GBDT

背景知识

CART

GBDT以CART（弱学习器）作为基分类器。在CART当中，采用基尼系数作为分裂标准，基尼系数是熵公式下的一阶展开[2]，衡量的是特征的不纯度，基尼系数越小越好，基尼的不纯度相当于熵所对应的混乱程度。

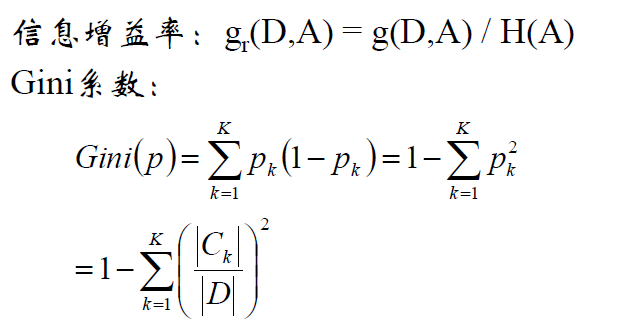
bagging & boosting

Bagging

即套袋法，其算法过程如下[1]：

A）从原始样本集中抽取训练集。每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行k轮抽取，得到k个训练集。（k个训练集之间是相互独立的）

B）每次使用一个训练集得到一个模型，k个训练集共得到k个模型。

C）对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）

Boosting

其主要思想是将弱分类器组装成一个强分类器。在PAC（概率近似正确）学习框架下，则一定可以将弱分类器组装成一个强分类器。

关于Boosting的两个核心问题：

1）在每一轮如何改变训练数据的权值或概率分布？

通过提高那些在前一轮被弱分类器分错样例的权值，减小前一轮分对样例的权值，来使得分类器对误分的数据有较好的效果。

2）通过什么方式来组合弱分类器？

通过加法模型将弱分类器进行线性组合，比如AdaBoost通过加权多数表决的方式，即增大错误率小的分类器的权值，同时减小错误率较大的分类器的权值。

而提升树通过拟合残差的方式逐步减小残差，将每一步生成的模型叠加得到最终模型。

将决策树与这些算法框架进行结合所得到的新的算法：

1）Bagging + 决策树 = 随机森林

2）AdaBoost + 决策树 = 提升树

3）Gradient Boosting + 决策树 = GBDT

GBDT

GBDT有两个版本，基于残差（传统GBDT）和基于梯度，在第三小节会解释为什么梯度版本会优于残差版本。

用于回归

输入是训练集样本$T={(x_1,y_1),(x_2,y_2),…(x_m,y_m)}$， 最大迭代次数T, 损失函数L。[3]

• adaboost是初始化样本个数作为权重
• gbdt是初始化y值均值作为权重

输出是强学习器f(x)

1) 初始化弱学习器

$$f_0(x) = argmin\sum_{i=1}^m L(y_i,c)$$

2) 对迭代轮数t=1,2,…T有：

• a)对样本i=1,2，…m，计算负梯度

$$r_{ti} = -\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)}_{f(x)=f_{t-1}(x)}$$

• b)利用$(x_i,r_{ti})(i=1,2,..m)​$，拟合一颗CART回归树，得到第t颗回归树，其对应的叶子节点区域为$R_{tj},j=1,2,…,J​$。其中J为回归树t的叶子节点的个数。
• c) 对叶子区域j =1,2,..J,计算最佳拟合值

$$c_{tj} = argmin \sum_{x_i∈R_{tj}} L(y_i,f_{t-1}(x_i)+c)$$

• d) 更新强学习器

$$f_t(x) = f_{t-1}(x)+\sum_{j=1}^J c_{tj} I(x∈R_{tj})$$

3) 得到强学习器f(x)的表达式

$$f(x) = f_T(x) = f_0(x)+\sum_{t=1}^T \sum_{j=1}^J c_{tj}I(x∈R_{tj})$$

用于分类

GBDT的分类算法从思想上和GBDT的回归算法没有区别，但是由于样本输出不是连续的值，而是离散的类别，导致我们无法直接从输出类别去拟合类别输出的误差。

为了解决这个问题，主要有两个方法，一个是用指数损失函数，此时GBDT退化为Adaboost算法。另一种方法是用类似于逻辑回归的对数似然损失函数的方法。也就是说，我们用的是类别的预测概率值和真实概率值的差来拟合损失。本文仅讨论用对数似然损失函数的GBDT分类。而对于对数似然损失函数，我们又有二元分类和多元分类的区别。本来仅写出多元分类的计算流程。

假设类别数为K，则此时我们的对数似然损失函数为：

$$L(y,f(x)) = -\sum_{k=1}^Ky_k logp_k(x)$$

其中如果样本输出类别为k，则$y_k=1$。第k类的概率$p_k(x)$的表达式为：

$$p_k(x) = exp(f_k(x))/\sum_{l=1}^K exp(f_l(x))$$

集合上两式，我们可以计算出第$t$轮的第$i$个样本对应类别$l$的负梯度误差为：

$$r_{til} = - [\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)}] _{f_k(x) = f_{l,t-1}(x)} = y_{il}-p_{l,t-1}(x_i)$$

　观察上式可以看出，其实这里的误差就是样本$i$对应$类别l$的真实概率和$t−1​$轮预测概率的差值。

对于生成的决策树，我们各个叶子节点的最佳负梯度拟合值为：

$$c_{tjl} = argmin \sum_{i=0}^m \sum_{k=1}^K L(y_k,f_{t-1,l}(x) + \sum _{j=0}^J c_{jl} I(x_i ∈ R_{tj})$$

负梯度拟合残差

为什么用负梯度拟合残差呢？

当损失函数为平方损失和时，负梯度=残差！

$$L(y,F(x)) = \frac{1}{2} (y-F(x))^2$$

注意到 $F(x_1),F(x_2),⋯,F(x_N) $就是一些数字，我们把 $F(x_i)$ 看作是参数，对它们求偏导数：

$$\frac{\partial J}{\partial F(x_i)} = \frac{\partial \sum_{i=1}^N(y_i,F(x_i))}{\partial F(x_i)} \\\\ =\frac{\partial (y_i,F(x_i))}{\partial F(x_i)} \\\\ = F(x_i)-y_i$$

当上式表明， 采用平方误差时，残差就是负梯度 ：

$$y_i-F(x_i) = -\frac{\partial J}{\partial F(x_i)}$$

平方损失函数(Square loss)有一个缺点：它对异常点(outliers)比较敏感。其它一些损失函数，如绝对损失函数(Absolute loss)，Huber loss 函数能更好地处理异常点。 下表是三种损失函数Square loss/Absolute loss/Huber loss对异常点的处理情况。

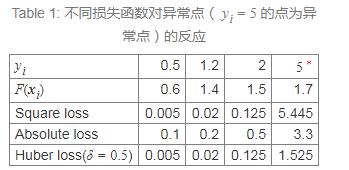
在前面的介绍中，我们知道采用Square loss为损失函数时，负梯度和残差相等。不过，当我们采用Absolute loss/Huber loss等其它损失函数时，负梯度只是残差的近似。

GBDT算法用梯度来取代残差。不过需要说明的是，这时新模型不再是 F+h（这个 h 是“残差”的拟合）了，而是 F+ρh （这个 h 是“负梯度”的拟合）。我们把负梯度称为伪残差(pseudo-residuals)。

为什么不直接使用残差，而使用负梯度呢（注：也有一些实现直接使用“残差”）？因为使用负梯度有时能够减小异常点的影响。 下面以Huber loss函数以例进行说明。

Huber loss (more robust to outliers)定义如下：

$$L(y,F) = \left\{ \begin{aligned} \frac{1}{2}(y-F)^2 , \ |y-F|\leq \delta \\\\ \delta(|y-F|-\delta/2),\ |y-F| > \delta \end{aligned} \right.$$

如果采用残差，则有：

$$h(x_i) = y_i -F(x_i)$$

如果是负梯度的话，则有：

$$h(x_i) = \frac{\partial (y_i,F(x_i))}{\partial F(x_i)} =\left\{ \begin{aligned} y_i-F(x_i) , \ |y-F|\leq \delta \\\\ \delta sign(y_i-F(x_i)),\ |y-F| > \delta \end{aligned} \right.$$

对比上面两式，可以发现，采用负梯度时异常点(会满足$|y−F|>δ$)产生的影响会变小。

RF与GBDT区别

（1）相同点

• 都是由多棵树组成
• 最终的结果都是由多棵树一起决定

（2）不同点

• 组成随机森林的树可以并行生成，而GBDT是串行生成
• 随机森林的结果是多数树表决的，而GBDT则是多棵树累加之和
• 随机森林对异常值不敏感，而GBDT对异常值比较敏感
• 随机森林是通过减少模型的方差来提高性能，而GBDT是减少模型的偏差来提高性能的（bagging是减少variance，而boosting是减少bias）

在实际应用中，通过梯度下降法求解的模型一般都是需要归一化的，比如线性回归、logistic回归、KNN、SVM、神经网络等模型。

但树形模型不需要归一化，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率，如决策树、随机森林(Random Forest)。

至于GBDT需不需要归一化呢？这个目前没有定论，看了一些答案似乎双方都有争论，所以还是需要在实际项目中多做尝试，如果归一化的代价比较大的话，就跳过；反之，加入归一化后，根据结果是否退化进行判断。

GBDT十大面试问题及解答

· gbdt 的算法的流程？
· gbdt 如何选择特征 ？
· gbdt 如何构建特征 ？
· gbdt 如何用于分类？
· gbdt 通过什么方式减少误差 ？
· gbdt的效果相比于传统的LR，SVM效果为什么好一些 ？
· gbdt 如何加速训练？
· gbdt的参数有哪些，如何调参 ？
· gbdt 实战当中遇到的一些问题 ？
· gbdt的优缺点 ？

答案来自：https://cloud.tencent.com/developer/article/1327985

XGBoost和GBDT的区别

1）将树模型的复杂度加入到正则项中，来避免过拟合，因此泛化性能会由于GBDT。

2）损失函数是用泰勒展开式展开的，同时用到了一阶导和二阶导，可以加快优化速度。

3）和GBDT只支持CART作为基分类器之外，还支持线性分类器，在使用线性分类器的时候可以使用L1，L2正则化。

4）引进了特征子采样，像RandomForest那样，这种方法既能降低过拟合，还能减少计算。

5）在寻找最佳分割点时，考虑到传统的贪心算法效率较低，实现了一种近似贪心算法，用来加速和减小内存消耗，除此之外还考虑了稀疏数据集和缺失值的处理，对于特征的值有缺失的样本，XGBoost依然能自动找到其要分裂的方向。

6）XGBoost支持并行处理，XGBoost的并行不是在模型上的并行，而是在特征上的并行，将特征列排序后以block的形式存储在内存中，在后面的迭代中重复使用这个结构。这个block也使得并行化成为了可能，其次在进行节点分裂时，计算每个特征的增益，最终选择增益最大的那个特征去做分割，那么各个特征的增益计算就可以开多线程进行。

参考文献：

[1]. Bagging和Boosting 概念及区别

[2]. 信息熵与基尼指数的关系（一阶泰勒展开）

[3]. GBDT小结

[4]. 方差和偏差

[5]. GBDT