word2vec

相关知识

GloVe与word2vec根据词汇的共现（co-occurrence）信息，将词汇编码成一个向量（所谓共现，即语料中词汇一块出现的频率）。两者最直观的区别在于，word2vec是predictive的模型，而GloVe是count-based的模型。

独热编码 离散编码，丢失了单词之间的相似性

词向量 分布式表达，能够编码词之间的关系

两种模型

SKip-gram 中心词预测上下文词的概率分布

CBOW 上下文词预测中心词的词向量

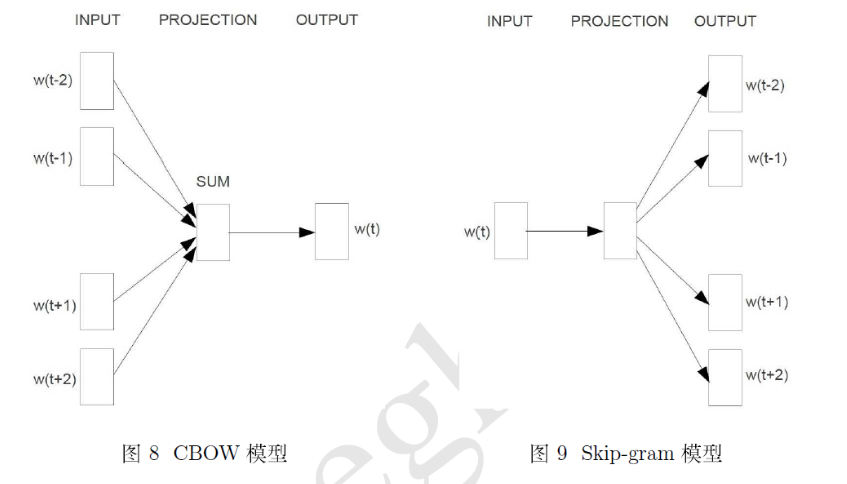
CBOW

假设训练语料为$D​$，选择一个窗口$m​$，根据上下文的单词c预测中心词t，使$P(w_t|w_c)​$最大。[2]

参数说明

• $w_i​$：词汇表V的单词$i​$，one_hot向量
• $V$：输入词的矩阵(n,|V|)
• $v_i$ ：$V$的第$i$列，单词$w_i$的输入向量
• $U$：输出词的矩阵(|V|,n)
• $u_i$：$U$的第i行，单词$w_i$的输出向量

神经网络

注意各个参数维度上的相乘

输入层 中心词的上下文单词生成one_hot词向量（$x^{t-m} ,…,x^{t-1},x^{t+1},…,x^{t+m}$）

投影层/隐藏层 将输入的上下文单词的向量叠加在一起并取平均值，作为最终的结果

$$v_c = V(\frac{x^{t-m} +...+x^{t-1}+x^{t+1}...+x^{t+m}}{2m})$$

输出层 将投影层的输出乘以$U​$，计算语义相似度向量，对其求概率分布

$$z = U·v_c \\\\ \hat{y} = P(w_t|w_c) = softmax(z) \\\\ = \frac{exp(u^T_t· v_c)}{\sum_{i=1}^{|V|} exp(u^T_i· v_c)}$$

损失函数

这里使用交叉熵作为中心词的损失函数：

$$J=-\sum_{t=1}^{|V|}y_t log(\hat{y_t})$$

y是one_hot向量，所以简化为：

$$J=-log(\hat{y_t})\\\\ = -log P(w_t|w_c) \\\\ = -log \frac{exp(u^T_t· v_c)}{\sum_{i=1}^{|V|} exp(u^T_i· v_c)}\\\\ =-u^T_tv_c +log\sum_{i=1}^{|V|} exp(u^T_i· v_c)$$

模型整体的损失函数为：

$$J = - \sum_{w_{t-m}^{t+m}∈D}log(\hat{y_t})$$

求导过程参考：[3]

评价

优点

CBOW比Skip-gram训练快

缺点

The movie is not very good , but i still like it .

The movie is very good , but i still do not like it .

I do not like it , but the movie is still very good .

其中第1、3句整体极性是positive，但第2句整体极性就是negative。如果只是通过简单的取平均来作为sentence representation进行分类的话，可能就会很难学出词序对句子语义的影响。

另外，CBOW会将context word 加起来， 在遇到生僻词时，预测效果将会大大降低。

Skip-gram

假设训练语料为$D​$，选择一个窗口$m​$，根据中心词t预测其上下文的单词c，使$P(w_c|w_t)​$最大，其实做法与CBOW大同小异。

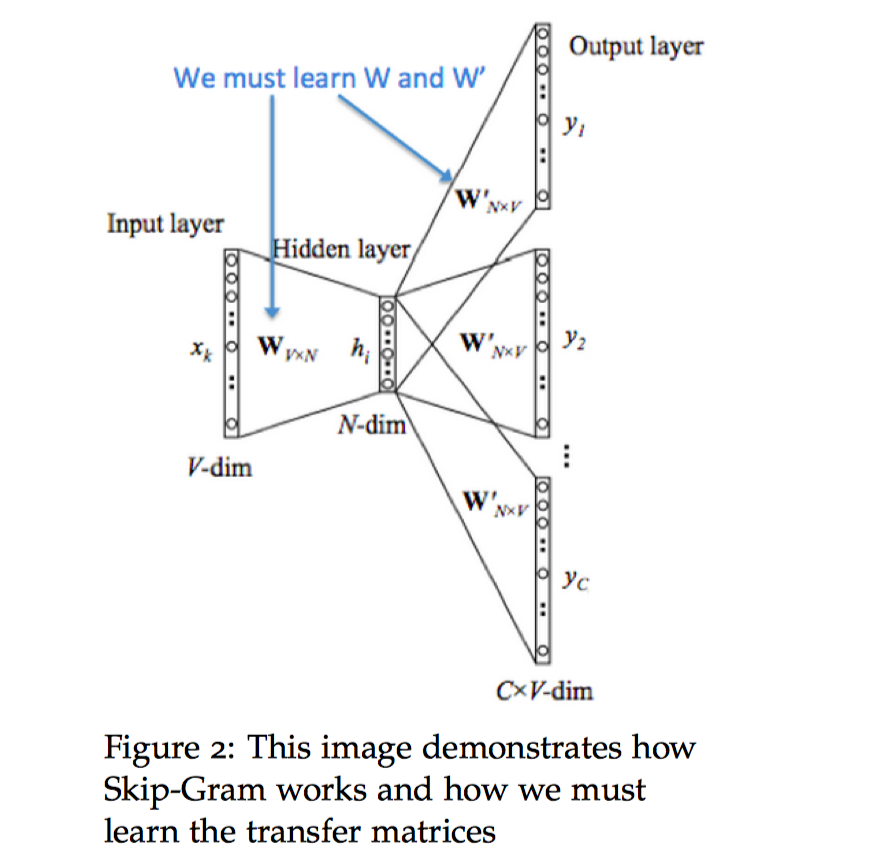
参数说明

• $w_i​$：词汇表V的单词$i​$，one_hot向量
• $V$：输入词的矩阵(n,|V|)
• $v_i$ ：$V$的第$i$列，单词$w_i$的输入向量
• $U$：输出词的矩阵(|V|,n)
• $u_i​$：$U​$的第i行，单词$w_i​$的输出向量

神经网络

输入层 生成中心词的one_hot词向量$x$

隐藏层/投影层 对中心词计算$v_t = Vx$

输出层 将投影层的输出乘以$U​$，计算语义相似度向量，对其求概率分布

$$z = U·v_t \\\\ \hat{y} = P(w_c|w_t) = softmax(z) \\\\ = \frac{exp(u^T_c· v_t)}{\sum_{i=1}^{|V|} exp(u^T_i· v_t)}$$

损失函数

不同于CBOW，由于该模型是预测多个词汇，所以选择引入朴素贝叶斯假设来拆分概率。给定中心词，各个输出的词是完全独立的，因此中心词$t$的损失函数为：

$$J = -log P(w_{t-m},...,w_{t-1},w_{t+1}...,w_{t+m}|w_t) \\\\ =-log \prod_{j=0,j≠ m}^{2m} P(w_{t-m+j}|w_t) \\\\ =-log \prod_{j=0,j≠ m}^{2m} \frac{exp(u^T_{t-m+j}· v_t)}{\sum_{i=1}^{|V|} exp(u^T_i· v_t)} \\\\ =-\sum_{j=0,j≠ m}^{2m} u^T_{t-m+j}· v_t +2m·log\sum_{i=1}^{|V|} exp(u^T_i· v_t)$$

注意对 $|V|​$ 的求和计算量是非常大的！任何的更新或者对目标函数的评估都要花费 $O(|V|)​$ 的时间复杂度，因此在实际过程中，需要寻找一些加速的技巧。

评价

优点

Skip-gram比CBOW更好地处理生僻字（出现频率低的字）

缺点

Skip-gram训练时间更长

加速方法

分层softmax 构建一棵huffman二叉树，计算所有词的概率来定义损失函数

负采样 抽取负样本来定义损失函数

负采样

在每一个训练的时间步，我们不去遍历整个词汇表，而仅仅是抽取一些负样例！考虑一堆中心词和上下文词(t,c)，如果这个词对来自语料库D（即c是t的上下文词），那么用$P(D=1|t,c)$表示，如果不是来自语料库，即$\tilde{D}$，用$P(D=0|t,c)$表示，其中$\theta$表示模型参数，即$U$和$V$。

$$P(D=1|t,c,\theta) = \sigma(u^T_tv_c) = \frac{1}{1+e^{-u^T_tv_c}}$$

采用极大似然估计得到：

$$J =P(D=1|t,c,\theta)\prod _{(t,c)∈\tilde{D}}P(D=0|t,c,\theta) \\\\ =P(D=1|t,c,\theta)\prod _{(t,c)∈\tilde{D}}(1-P(D=1|t,c,\theta))\\\\ logJ=logP(D=1|t,c,\theta)+\sum_{(t,c)∈\tilde{D}}log(1-P(D=1|t,c,\theta)) \\\\ =log \frac{1}{1+e^{-u^T_tv_c}} +\sum_{(t,c)∈\tilde{D}}log(1-\frac{1}{1+e^{-u^T_tv_c}}) \\\\ =log \frac{1}{1+e^{-u^T_tv_c}} +\sum_{(t,c)∈\tilde{D}}log(1+\frac{1}{1+e^{u^T_tv_c}})$$

那么某个单词的损失函数就是：

$$J = - log \frac{1}{1+e^{-u^T_tv_c}} -\sum_{(t,c)∈\tilde{D}}log(1+\frac{1}{1+e^{u^T_tv_c}})$$

Skip-gram

我们对给定中心词$t$来观察的上下文单词$c−m+j$的新目标函数为：

$$-log \sigma (u_{t-m+j}^T·v_t)-\sum_{k=1}^Klog \sigma(-\tilde{u_k}·v_t)$$

CBOW

我们对给定上下文向量$v_c = V(\frac{x^{t-m} +…+x^{t-1}+x^{t+1}…+x^{t+m}}{2m})$来观察中心词的新目标函数为：

$$- log \sigma(u_t^T·v_c)-\sum_{k=1}^Klog \sigma(-\tilde{u_k}·v_t)$$

在上面的公式中，$\tilde{u_k}∣k=1…K$是从$P(w)$ 中抽样。在Tensorflow中，通常会用到nce_loss或者sample_loss。

分层softmax

Hierarchical Softmax相比普通的 Softmax这是一种更有效的替代方法。在实际中，Hierarchical Softmax 对低频词往往表现得更好，负采样对高频词和较低维度向量表现得更好。

Hierarchical Softmax使用一个二叉树来表示词表中的所有词。树中的每个叶结点都是一个单词，而且只有一条路径从根结点到叶结点。在这个模型中，没有词的输出表示。相反，图的每个节点（根节点和叶结点除外）与模型要学习的向量相关联。

从根节点出发，到达指定叶子节点的路径是唯一的。Hierarchical Softmax正是利用这条路径来计算指定词的概率，而非用softmax来计算。

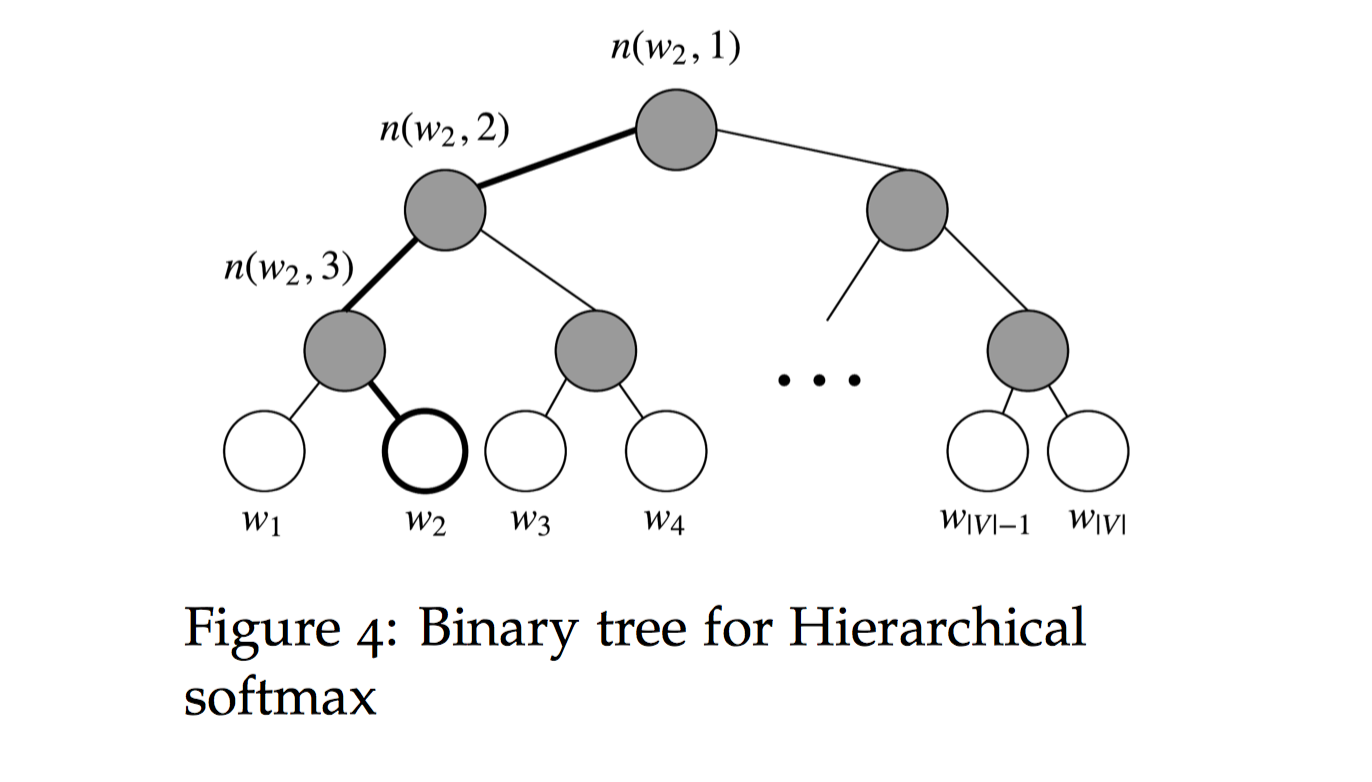
从根节点出发，走到指定叶子节点$w$的过程，就是一个进行 $L(w)−1$次二分类的过程，$L(w)$为根节点到该叶子节点的路径长度，如$L(w_2)=4$：路径上的每个非叶子节点都拥有两个孩子节点，从当前节点$ n(w,j)$j) 向下走时共有两种选择，走到左孩子节点$ ch(n(w,j))$ 就定义为分类到了正类，走到右孩子节点就定义为分类到了负类。

CBOW

隐藏层的输出为$v_c$，用二项Logistic回归模型对每一次分类过程建模：从当前节点$n(w,j)$走到下一节点，那么走到左孩子节点的概率为：$\sigma(u_{n(w,j)}^T v_c)$，那么走到右孩子节点的概率为：$1-\sigma(u_{n(w,j)}^T v_c) = \sigma(-u_{n(w,j)}^T v_c)$。将上式统一起来就是：

$$\sigma([[n(w,j+1)=ch(n(w,j))]](u_{n(w,j)}^T v_c))$$

如果括号为真，则输出1，反之输出-1。那么中心词的概率表示为：

$$P(w_t|w_c)\\\\ =P(w_t|w_{t-m},...,w_{t-1},w_{t+1},...,w_{t+m}) \\\\ =\prod_{j=1}^{L(w)-1} \sigma([[n(w,j+1)=ch(n(w,j))]](u_{n(w,j)}^T v_c))$$

Skip-gram

$$P（w_c|w_t） \\\\ =\prod_i \prod_{j=1}^{L(w)-1} \sigma([[n(w,j+1)=ch(n(w,j))]](u_{n(w,j)}^T v_{t+i})) \\\\ i∈\{-m,...,m\}$$

矩阵分解

所谓而分布式表示，就是开一个窗口（前后若干个词加上当前词，作为一个窗口），统计当前词的前后若干个词的分布情况，就用这个分布情况来表示当前词，而这个分布也可以用相应的$N$维的向量来表示。由于是通过上下文分布来表示一个词，而不再是孤立地“独热”了，因此能够表示语义的相关性，但问题是它还是$N$维的，维度还是太大了，整个词向量表（共现矩阵）太稀疏。[4]

对于稀疏矩阵，一个既能够将维，又可以提高泛化能力的方案就是对矩阵SVD分解。这种方案就是说：原始的分布式表示的词向量是$N$维的，太大，我们可以用自编码器来降低维度，自编码器的中间节点数记为$n$，把$n$设置为一个适当的值，训练完自编码器后，直接把中间层的$n$维结果就作为新的词向量。所以说，这就是一个$N$维输入，中间节点为$n$个，$N$维输出的自编码器方案，也等价于一个SVD分解（SVD分解等价于一个不带激活函数的三层自编码器）。

简单自编码器：第一层：m x hidden_size，第二层：hiddex_size x n

SVD：第一层：mxm，第二层：mxn，第三层：nxn

word2vec：第一层：embed_size x vocab_size，第二层：vocab_size x embed_size

input_size = 784
hidden_size = 64
output_size = 784

x = Input(shape=(input_size,))

# Encoder
h = Dense(hidden_size, activation='relu')(x)

# Decoder
r = Dense(output_size, activation='sigmoid')(h)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')

Word2Vec的一个CBOW方案是，将前后若干个词的词向量求和，然后接一个$N$维的全连接层，并做一个softmax来预测当前词的概率。这种词向量求和，等价于原来的词袋模型接一个全连接层（这个全连接层的参数就是词向量表），这样来看，Word2Vec也只是一个$N$维输入，中间节点为$n$个，$N​$维输出的三层神经网络罢了，所以从网络结构上来看，它跟自编码器等价，也就是跟SVD分解等价。

从实现上来看，区别也很明显：

1、Word2Vec的这种方案，可以看作是通过前后词来预测当前词，而自编码器或者SVD则是通过前后词来预测前后词；

2、Word2Vec最后接的是softmax来预测概率，也就是说实现了一个非线性变换，而自编码器或者SVD并没有。

代码

简单的代码片段：

with tf.device('/cpu:0'):
    # Create the embedding variable (each row represent a word embedding vector)
    embedding = tf.Variable(tf.random_normal([vocabulary_size, embedding_size]))
    # Lookup the corresponding embedding vectors for each sample in X
    X_embed = tf.nn.embedding_lookup(embedding, X)

    # Construct the variables for the NCE loss
    nce_weights = tf.Variable(tf.random_normal([vocabulary_size, embedding_size]))
    nce_biases = tf.Variable(tf.zeros([vocabulary_size]))

# Compute the average NCE loss for the batch
loss_op = tf.reduce_mean(
    tf.nn.nce_loss(weights=nce_weights,
                   biases=nce_biases,
                   labels=Y,
                   inputs=X_embed,
                   num_sampled=num_sampled,
                   num_classes=vocabulary_size))

参考文献：

[1]. word2vec数学原理

[2]. cs224n notes_1

[3]. 词表示模型

[4]. SVD分解