循环神经网络

RNN

基本结构

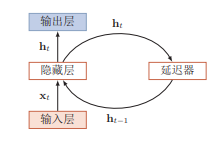
在前馈神经网络中，隐藏层的节点之间是无连接的，而简单循环网络增加了从隐藏层到隐藏层的反馈连接。

RNN本质上是一个递推函数，假设在时刻$t$，隐藏层的状态为$h_t$，此时隐藏层不仅和当前时刻的输入$x_t$有关，还和上一个时刻的隐层状态$h_{t-1}$ 有关。

$$h_t = f(U x_t+ W h_{t-1}+ b)\\\\ o_t=g(V*h_t)$$

$f(·)​$和$g(·)​$是非线性激活函数，通常为Tanh函数和Softmax函数。

初始$h_0$：init_state = tf.zeros([batch_size, hidden_dim])

维度解释

• input_dim：输入向量的维度，hidden_dim：隐藏层的维度，output_dim：输出向量的维度

• $x_t$：max_len，word_dim，U：hidden_dim，word_dim

• W：hidden_dim，hidden_dim，$h_t$：max_len+1，hidden_dim

• V：output_dim，hidden_dim，$o_t​$：max_len，output_dim

几种模式

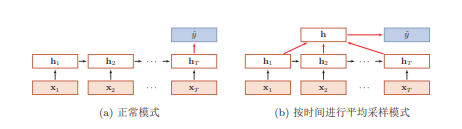
序列到类别

• 产生固定大小的表示，用于下一步处理

• 主要用于序列数据的分类问题，输入为单词的序列，输出为该文本的类别

• $$\hat{y} = g(h_T)$$

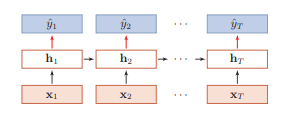
同步的序列到序列

• 每一刻都有输入和输出，输入序列和输出序列的长度相同

• 主要用于序列标注任务

• $$\hat{y_t} = g(h_t)，\ t∈[1,T]$$

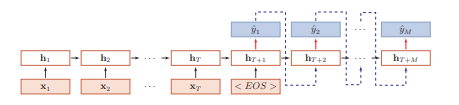
异步的序列到序列

• 输入序列和输出序列不需要严格的对应关系，也不需要保持相同的长度

• 也被称为编码器-解码器

• $$h_t = f_1(h_{t-1},x_t)， \ t∈[1,T]\\\\ h_{T+t} = f_2(h_{T+t-1},\hat{y_{t-1}})， \ t∈[1,M] \\\\ \hat{y_t} = g(h_{T+t})， \ t∈[1,M]$$

反向传播

反向传播参考链接：rnn-grad-deriv.pdf

参数共享

不同时刻t中的参数计算（$U、V、W​$）是一样的，即在序列数据的时刻之间共享参数。共享参数使得模型的复杂度大大减少，并使RNN可以适应任意长度的序列，带来了更好的可推广性。但是RNN 因为每一个时间步都共享参数的缘故，容易出现梯度消失或者梯度爆炸。

$$h_t = f(U x_t+ W h_{t-1}+ b)\\\\ \frac{\partial h_{k+1}}{\partial h_k} = diag(f'(U x_i + W h_{i-1}))W \\\\ \frac{\partial h_t}{\partial h_i} = \prod_{k=i}^{t-1}\frac{\partial h_{k+1}}{\partial h_k} \\\\ \frac{\partial h_k}{\partial h_1} = \prod_i^k diag(f'(U x_i + W h_{i-1}))W$$

因为循环神经网络经常使用非线性函数为Tanh或者Sigmoid，$f’(x)$永远小于1，所以梯度消失的情况更普遍些，应当重点关注。

梯度消失

原因

• 激活函数（Sigmoid，Tanh）
• 梯度连乘

如何解决

• relu
• 残差结构
• 门控机制（LSTM、GRU）
• 矩阵初始化

评价

优点 为处理时序数据提供了短期记忆能力

缺点 造成梯度爆炸和梯度消失，如果需要的历史信息距离当前位置很远，则RNN无法学习到过去的信息，于是导致无法长期依赖。

LSTM

LSTM与传统RNN的对比

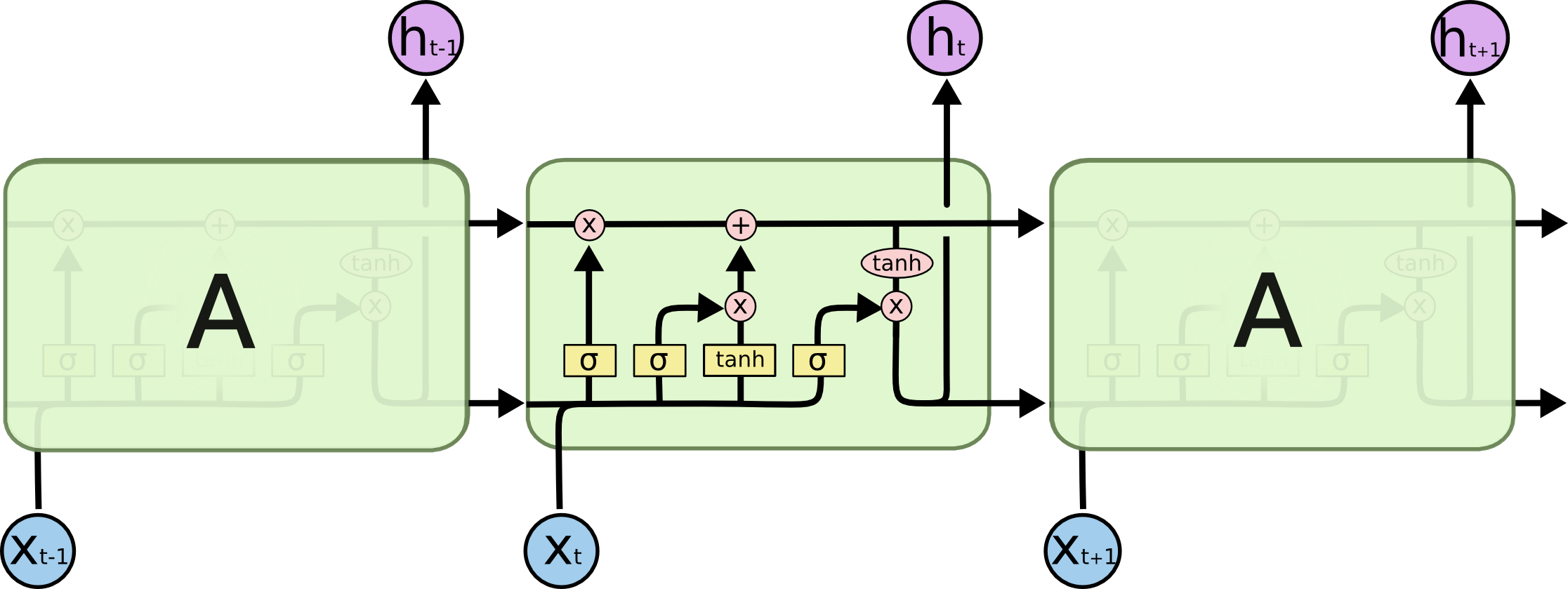
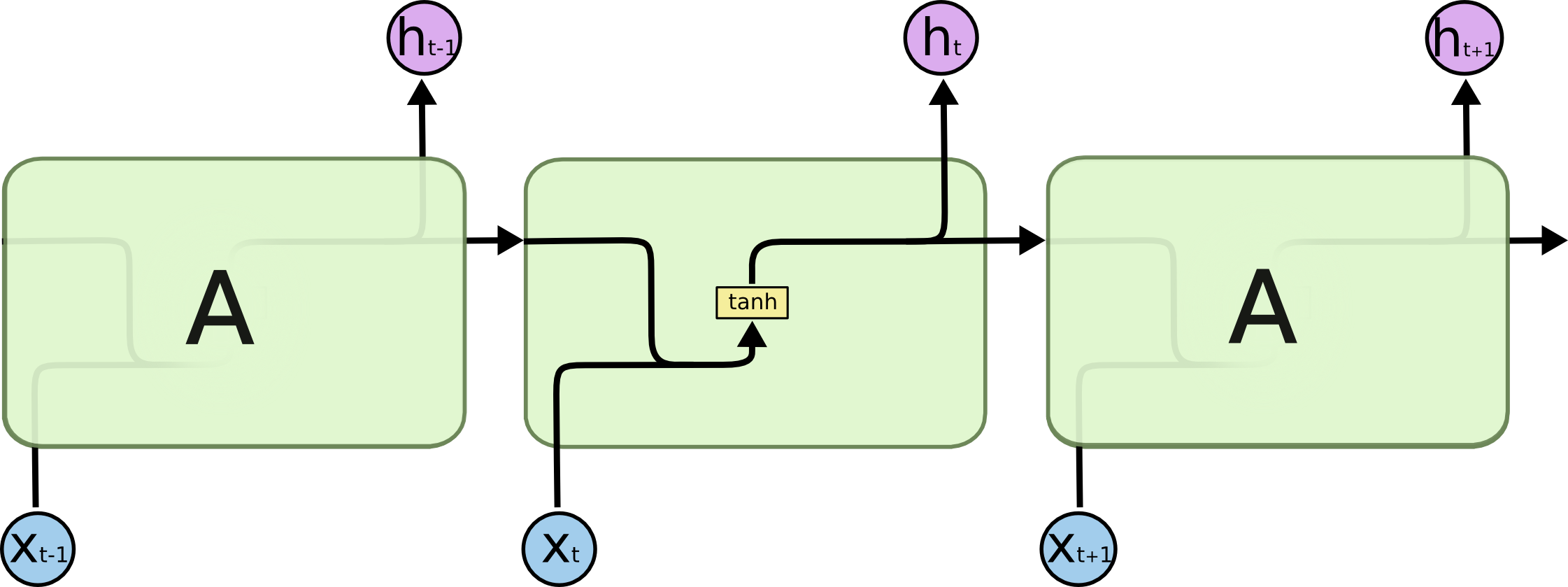
网络架构

几种信息

输入信息 $x_t$ 当前时刻的输入信息

隐藏状态信息(短时记忆) $h_t​$ 对长时记忆进行变换，在简单循环网络中，隐状态每个时刻都会被重写，因此可以看作是一种短期记忆

长时记忆 $c_t$ 由上一个长时记忆和候选状态(新的记忆信息)联合而成

候选状态 c˜t 由当前信息和上一个时刻的短时记忆变换而成

门结构

LSTM单元中有三种调节信息流的门结构：遗忘门、输入门和输出门。

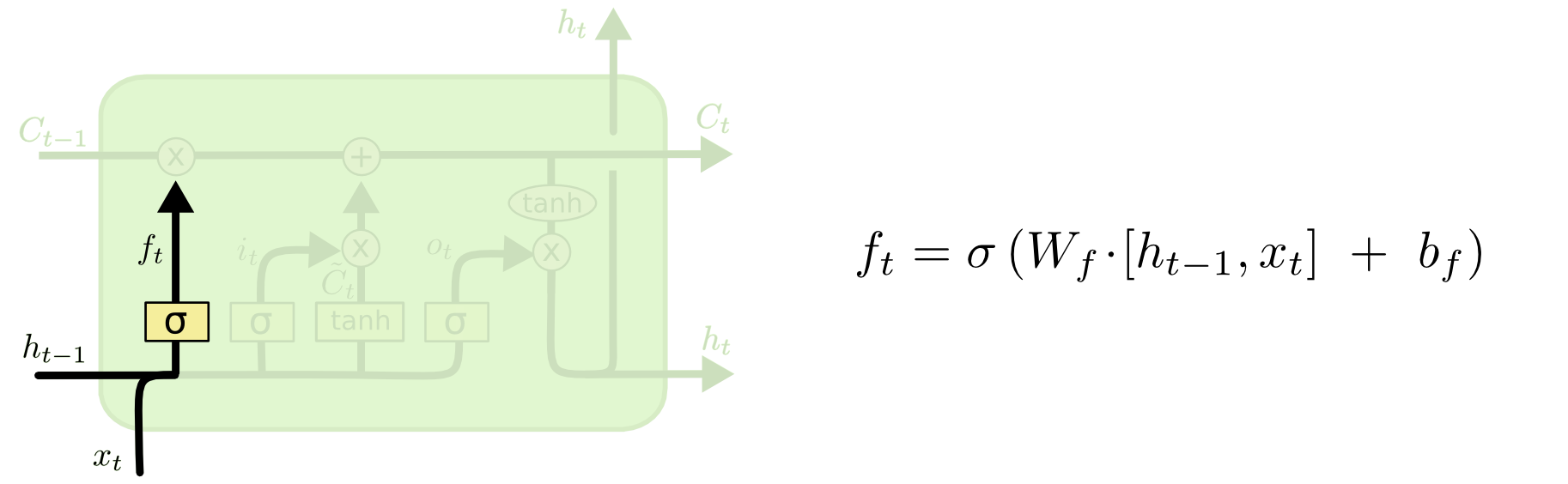
遗忘门 $f_t$控制上一个时刻的长时记忆$c _ { t - 1 }$需要遗忘多少信息

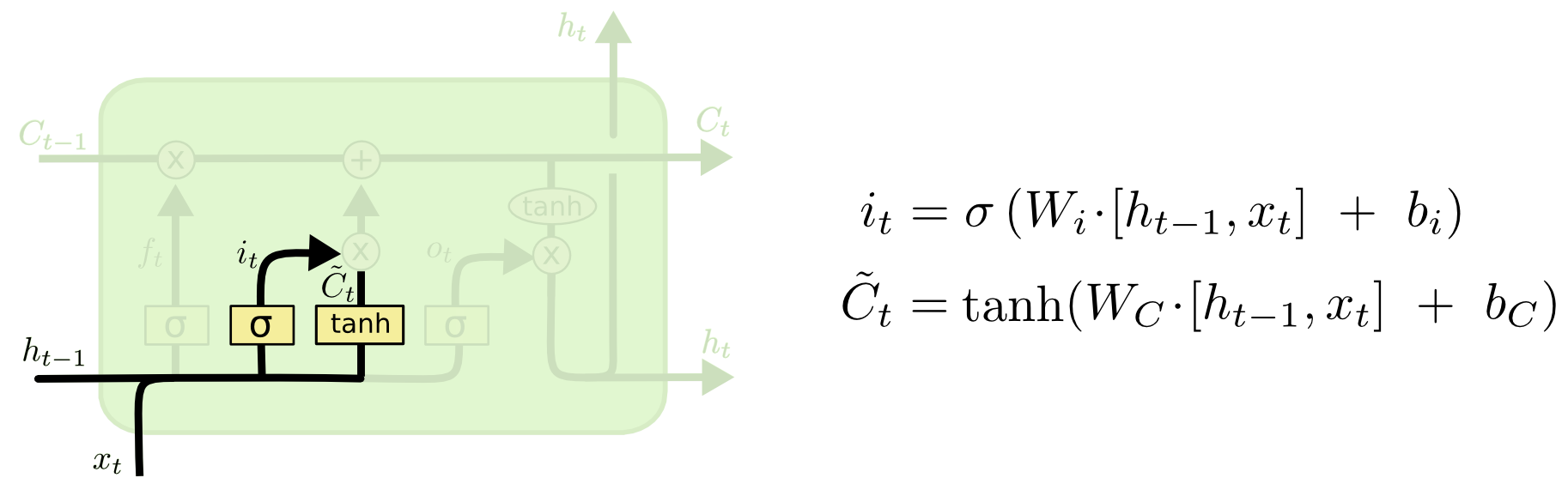
输入门与候选状态 $i_t$ 控制当前时刻的候选状态c˜t 有多少信息需要保存（同样的信息，计算Sigmoid是保存比例，计算Tanh是得到新的信息）

长时记忆

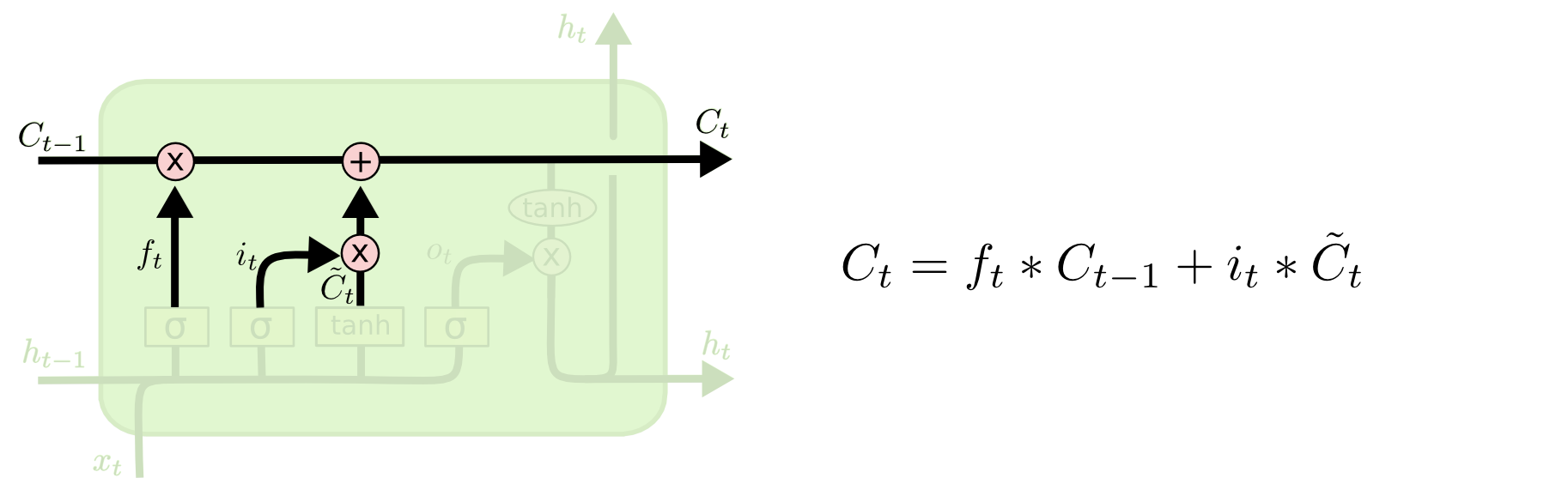
输出门与短时记忆 $o_t$控制当前长时记忆$c_t$有多少信息需要输出给$h_t$

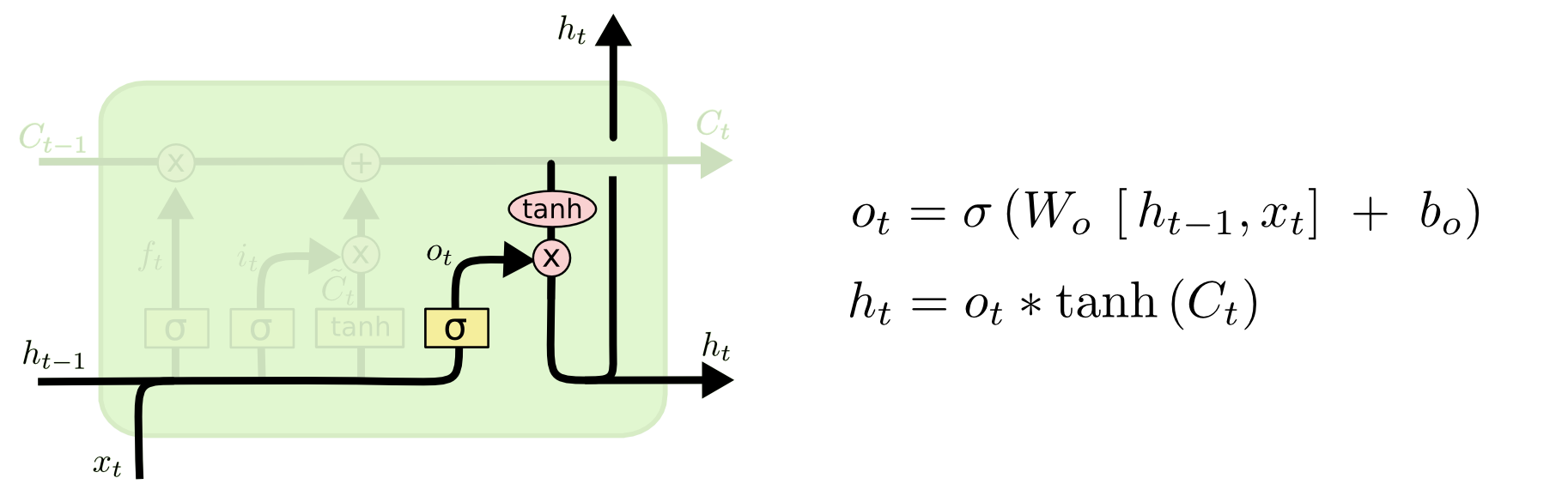
LSTM中的Tanh和sigmoid函数

两种函数的功能并不一样。

1. sigmoid 用在了各种gate上，产生0~1之间的值，这个一般只有sigmoid最直接了。通过这样，网络能了解哪些数据不重要需要遗忘，哪些数字很重要需要保留。
2. tanh 用在了状态和输出上，是对数据的处理，这个原始论文是使用sigmoid，但是后来换成了Tanh。Tanh函数能让输出位于区间(-1, 1)内，从而调节神经网络输出。对于LSTM和GRU来说，Tanh函数是对原来的输入信息做了一种变换。

解决梯度消失的原因

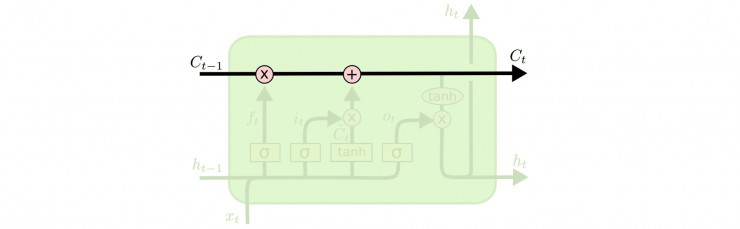
对$c_t = fc_{t-1}+i \tilde{c_t}$ 求梯度$\frac{\partial c_t}{\partial c_{t-1}}$，根据求导法则求解如下：[1]

$$\frac{\partial c_t}{\partial c_{t-1}} = \frac{\partial c_t}{\partial f_t}\frac{\partial f_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial c_{t-1}} + \frac{\partial c_t}{\partial i_t}\frac{\partial i_t}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial c_{t-1}} +\frac{\partial c_t}{\partial \tilde{c_t}}\frac{\partial \tilde{c_t}}{\partial h_{t-1}}\frac{\partial h_{t-1}}{\partial c_{t-1}} + \frac{\partial c_t}{\partial c_{t-1}}$$

重新整理：

$$\frac{\partial c_t}{\partial c_{t-1}} = c_{t-1} \sigma'(·)W_f*o_{t-1}tanh'(c_{t-1}) \\\\ +\tilde{c_t}\sigma'(·)W_i*o_{t-1}tanh'(c_{t-1}) \\\\ + i_t tanh'(·)W_c *o_{t-1}tanh'(c_{t-1}) \\\\ +f_t$$

注意以上梯度和RNN梯度消失的区别，在RNN中，$\frac{\partial h_t}{\partial h_{t-1}}$的结果要么全部大于1，要么全部在[0,1]之间（will eventually take on a values that are either always above 1 or always in the range [0,1]），这是导致梯度消失的原因所在。而$\frac{ \partial c_t}{\partial c_{t-1}}$，在任何时候都可以大于1或者在[0,1]之间（at any time step can take on either values that are greater than 1 or values in the range [0,1]），因此在多个时刻之后，它不会收敛与0或者无穷大。

This might all seem magical, but it really is just the result of two main things:

• The additive update function for the cell state gives a derivative thats much more ‘well behaved’
• The gating functions allow the network to decide how much the gradient vanishes, and can take on different values at each time step. The values that they take on are learned functions of the current input and hidden state.

LSTM变体

无遗忘门的LSTM

亦被称为Origin LSTM，Hochreiter and Schmidhuber [1997]最早提出的LSTM网络是没有遗忘门的，其内部状态的更新为：

$$c_t = c_{t-1} +i_t *\tilde{c_t}$$

当输入序列的长度非常大时，长时记忆c会不断增大，记忆单元的容量会饱和，从而大大降低LSTM模型的性能。

观察口连接

观察口连接，把观察到的单元状态也连接sigmoid上。

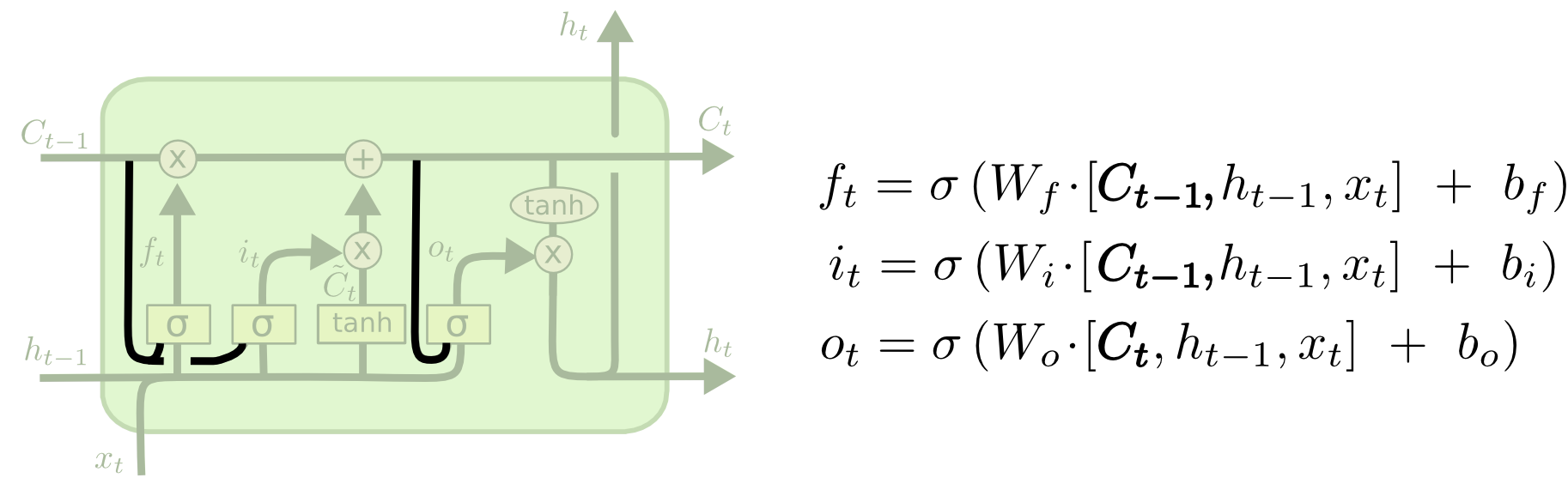
耦合输入门和遗忘门

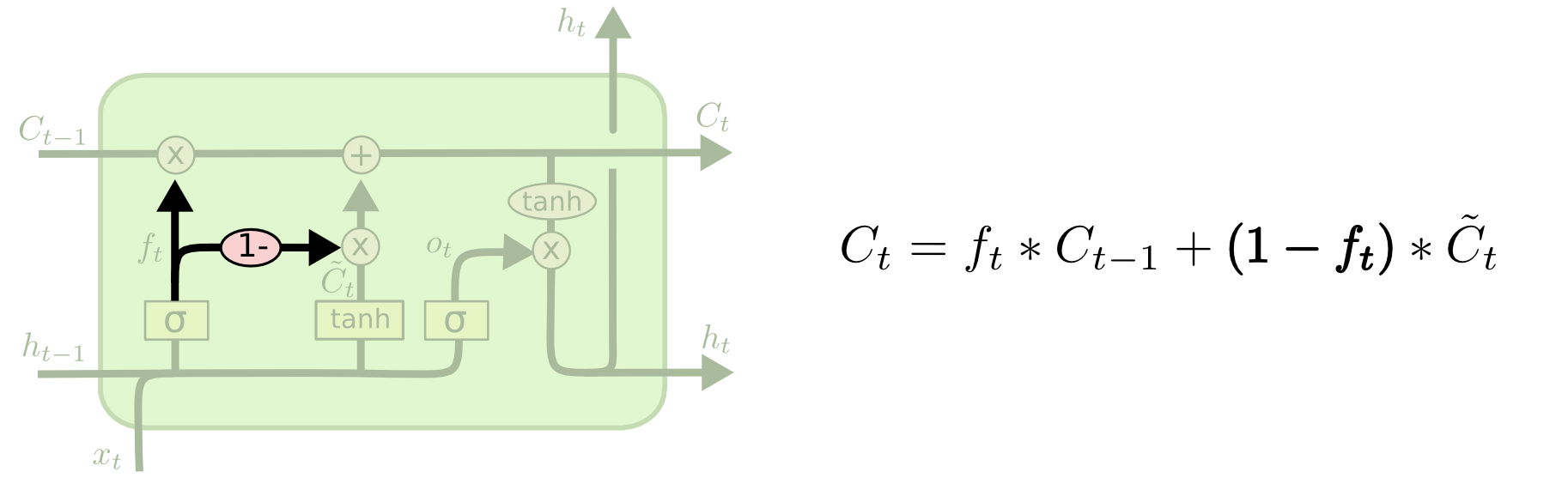
LSTM网络中的输入门和遗忘门有些互补关系，因此同时用两个门比较冗余。为了减少LSTM网络的计算复杂度，将这两门合并为一个门。令$i_t = 1-f_t$，更新如下：

GRU

GRU网络也是引入门机制来控制信息更新的方式。

与LSTM比较

GRU将输入门与和遗忘门合并成一个门：更新门。同时，GRU也不引入额外的记忆单元，在当前状态信息$h_t$和历史状态信息$h_{t-1}​$ 之间引入线性依赖关系，直接用隐藏状态传递信息。

网络架构

几种信息

输入信息 $x_t​$ 当前时刻的输入信息

当前状态信息 $h_t$ 由历史状态信息和候选状态(新的记忆信息)联合而成

候选状态 $\tilde{h_t}$ 由当前状态和历史状态信息变换而成

历史状态信息 $h_{t-1}​$

门结构

重置门 $r_t$ 用于控制忽略历史状态信息的程度

• r = 0时，候选状态$\tilde{h_t} = tanh(W x_t)$只和当前输入$x_t$ 相关，和历史状态信息无关

• r = 1时，候选状态$\tilde{h_t}= tanh(W·[x_t,h_{t−1} ])​$和当前输入$x_t​$ 和历史状态信息$h_{t−1}​$ 相关，和简单循环网络一致

更新门 $z_t$ 用于控制历史状态信息被融合到当前状态信息中的程度

• z = 0 时，当前状态 ht 和历史状态信息$h_{t−1}$之间为非线性函数

1. 同时有z = 0, r = 1时，GRU网络退化为简单循环网络
2. 同时有z = 0, r = 0时，当前状态信息$h_t$ 只和当前输入$x_t$ 相关，和历史状态信息$h_{t-1}$ 无关

• z = 1时，当前状态信息$h_t = h_{t−1}$等于历史状态信息$h_{t−1}$，和当前输入$x_t$ 无关

与RNN比较

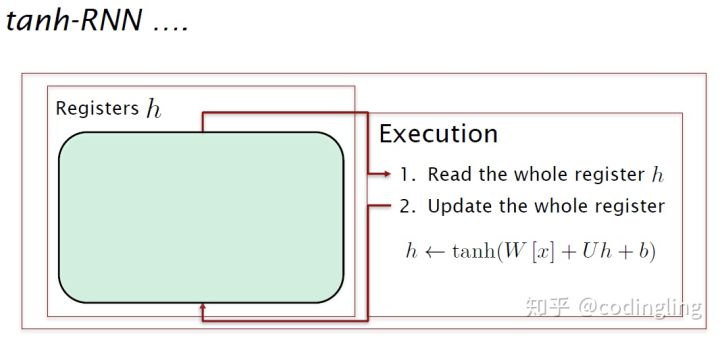
RNN寄存器，读取所有寄存器，运算后存入所有寄存器，没有灵活性。

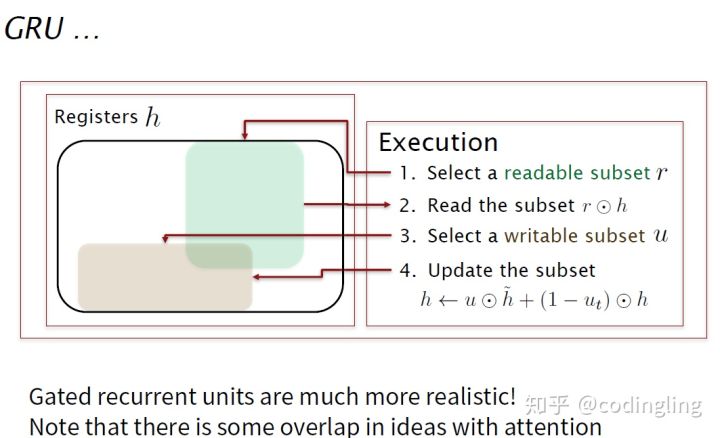
GRU寄存器，允许你灵活地学习。可以有选择地读取子集，有选择地写入，也就是选择读取部分寄存器，执行运算，写入部分寄存器。这里一个门是选择读取子集的什么内容（Reset Gate），另一个门是去重写哪些部分的隐藏状态（Update Gate）。

深层RNN

所谓深层RNN网络，是指超过两层的RNN网络。对于单层双向RNN网络，结构如下：

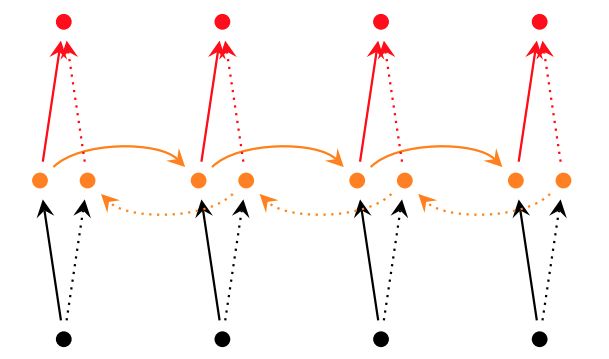
而对于深层双向RNN网络，主要有2种不同的实现：

tf.nn.bidirectional_dynamic_rnn

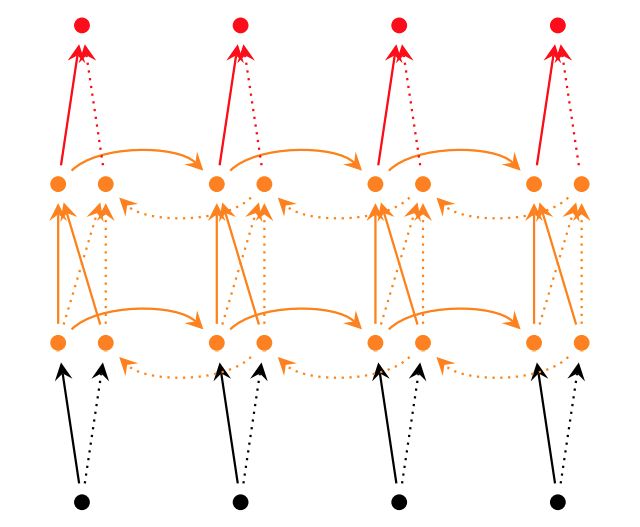
tf.contrib.rnn.stack_bidirectional_dynamic_rnn

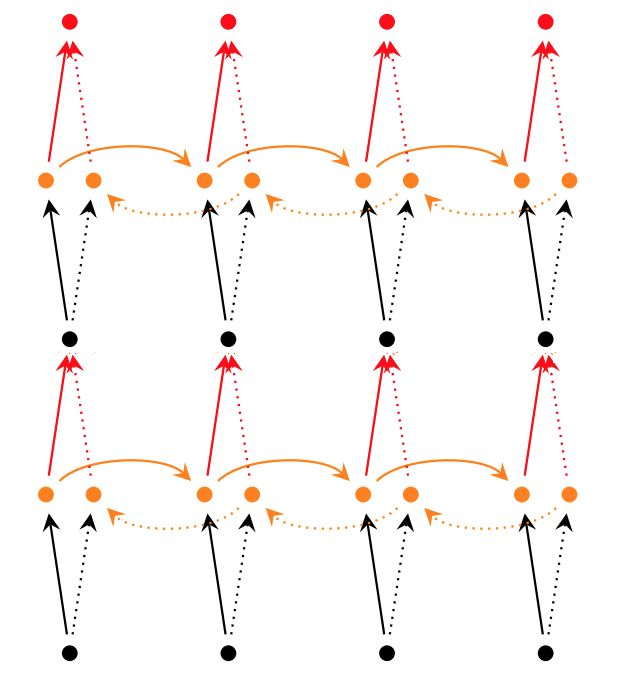
参考文献：

[1]. LSTM与梯度消失

[2]. https://zhuanlan.zhihu.com/p/30465140

[3].