网络优化

神经网络会遇到许多困难：

• 数据集的问题包括：不平衡数据集，数据集的大小，训练测试的分布不一致，数据质量（数据清洗）

• 对于浅层的神经网络来说，其困难主要来自于凸问题（优化问题）

• 深层神经网络的困难则是为了防止过拟合（泛化问题），超参数优化，梯度消失，当然还有加快性能

凸问题

为什么有凸优化问题

ML/DL在计算模型中都在寻找全局最优解，那么如果损失函数为凸函数，意味着存在全局的最小值，如果是非凸的，则找不到全局最小值。

大多数DL中损失函数都是非凸的[2]，其非凸为什么很难优化？[1]

持续好多年，学术界认为DL在优化的时候包含很多局部极小值，使得优化算法容易陷入到这些局部极小值点中，难以自拔。2014年NIPS的文章《Identifying and attacking the saddle point problem in high-dimensional non-convex optimization》中提出，高维非凸优化的困难之处在于存在大量鞍点（ 鞍点是梯度为0，但一些维度是最高点，另一些维度是最低点）而非局部极小值。

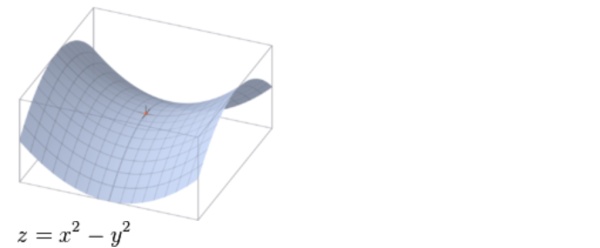
梯度优化算法在鞍点附近，梯度很小，Loss变化很小，形成“卡住了”的现象（而且针对高维情形，鞍点附近的平坦区域可能非常大）。这种现象和局部极小值处的现象一致，或许这就是导致学术界很长一段时间认为高维非凸优化困难的原因是存在大量局部极小值的原因。二者的区别在于，虽然“卡住了”，但是还是可以从鞍点出走出来（加扰动），有可能进入另一个鞍点附近，但是局部极小值不可以！

在机器学习领域中，非凸优化中的一个核心问题是鞍点的逃逸问题，研究表明，梯度下降法一般可以渐近地逃离鞍点。梯度下降法（Gradient descent）是一个一阶最优化算法， 要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索，则会接近函数的局部极大值点；这个过程则被称为梯度上升法。

梯度下降法如何处理：

• 预处理

• 初始化

• 学习率

• 梯度下降法的变种

数据预处理

在我们面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛。

以房价问题为例，假设我们使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0-2000平方英尺，而房间数量的值则是0-5，以两个参数分别为横纵坐标，绘制代价函数的等高线图能，看出图像会显得很扁，取值范围大的特征会占主导作用，梯度下降算法需要非常多次的迭代才能收敛。

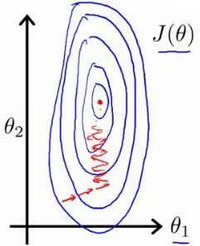
解决的方法是尝试将所有特征的尺度都尽量缩放到-1到1之间。如图：

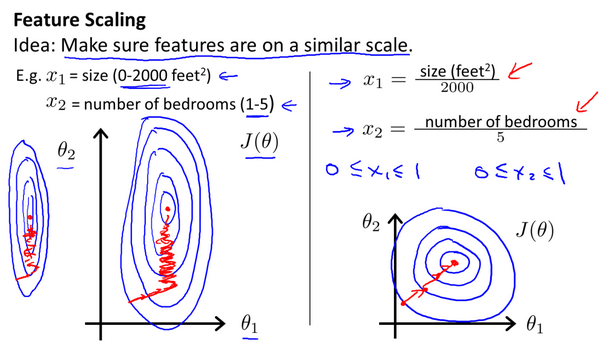
标准化归一法 令：$x= \frac {x-\mu}{s}$，其中$\mu$是平均值，$s$是标准差。

极大极小值归一法 $x = \frac{x - x_{min}}{x_{max}-x_{min}}$

初始化

当你训练神经网络时，权重随机初始化是很重要的。对于逻辑回归，把权重初始化为0当然也是可以的。但是对于一个神经网络，如果你把权重或者参数都初始化为0，那么梯度下降将不会起作用。具体来说，在连接到相同输入的隐藏层中并排的节点必须有不同的权重，这样才能使学习算法更新权重。 这通常被称为在训练期间需要打破对称性（symmetry）。

Glorot Initialization(glorot_uniform, glorot_normal)

Glorot Initialization，或者叫 Xavier Initialization，是Xavier Glorot和Yoshua Bengio于2010年提出的初始化方法，该方法的均匀分布版本(glorot_uniform)是Keras中全连接层、二维卷积/反卷积层等层的默认初始化方式。[3]

假设给定神经元接收n个输入数据$x =[x_1,x_2,…,x_n]$， 并且输出表示为$y$， 权值表示为$w$ . 则有以下公式：

$$y = w_1 x_1 + w_2 x_2 +...+ w_n x_n + b$$

其中$b$表示神经元的偏置（bias），由于这里输入数据$x$与权值$w$相互独立，因此对于以上公式中任意一项$w_i x_i$，其方差$Var(w_i x_i)$可表示为：

$$Var(w_i x_i) = E[x_i]^2Var(w_i) + E[w_i]^2Var(x_i) +Var(x_i)Var(w_i)$$

这里，如果输入数据已经进行预处理从而使其具有0均值，而且假设权向量的均值也为0，那么以上公式将简化为：

$$Var(w_i x_i) = Var(x_i)Var(w_i)$$

如果更进一步，假设$x_i$与$w_i$独立同分布，那么由以上公式可计算出神经元输出$y$的方差为：

$$Var(y) = Var(w_1 x_1 +w_2 x_2 +...+w_n x_n + b) \\\\ = Var(w_1 x_1) + ... + Var(b) \\\\ = nVar(x_i)Var(w_i)$$

在这里, 我们用$y^{(l)}$来表示第l 层的输出, $n^{(l)}$ 表示该层的输入数据维度，并且使用 $w^{(l)}$表示该层的神经元权值。那么，最后一层（表示为$L^{th}$）的输出方差将可以通过以下方式计算：

$$Var(y^{(L)}) = n^{(L)}Var(y^{(L-1)})Var(w^{(L)}) \\\\ = n^{(L)}[n^{(L-1)}Var(y^{(L-2)})Var(w^{(L-1)})]Var(w^{(L)}) \\\\ =....\\\\ =Var(x)\prod ^L_{l=1} [n^{(l)}Var(w^{(l)})]$$

在以上公式中，中间的连乘项，$\prod ^L_{l=1} [n^{(l)}Var(w^{(l)})]$，是导致深层网络难以优化的一个重要原因。如果其中的每项都小于1，那么一定深度后将会无限趋近于零。另一方面，如果每项都大于1的话，用不了几层就会大到可能越界。因此，为了使得x与y具有相同均值和方差，$n^{(l)}Var(w^{(l)})=1$，权值矩阵的方差则要求$Var(w^{(l)}) = \frac {1}{n^{(l)}}$，类似的，以相同的方式考虑反向传播过程，应当保持$Var(w^{(l)}) = \frac {1}{n^{(l+1)}}$，其中n(l+1)表示该层的输出（即下一层网络的输入）维度。为了综合考虑输入与输出，对正向与反向过程提取调和平均数，即

$$Var(w^{(l)}) = \frac {2}{n^{(l)} + n^{(l+1)}}$$

因此对于正态分布，当输入数据具有0均值与单位方差时只需要按照以上公式调整方差即可。对于均匀分布X∼U[a,b]，其方差计算方式为

$$Var(x) = \frac {(b-a)^2} {12}$$

因此，为保证0均值与单位方差，权值$w$的分布应满足：$w^{(l)}$~ $U[- \frac { \sqrt 6}{n^{(l)} + n^{(l+1)}},\frac { \sqrt 6}{n^{(l)} + n^{(l+1)}}]$

He Initialization(he_normal, he_uniform)

这两种初始化策略由微软亚洲研究院的何凯明等人于2015年正式发表，其基本思路与Glorot方法一致，即通过对权值进行缩放以完成normalization，与Glorot方法不同的是，该方法只考虑前向过程，因此对于正态分布和均匀分布，其公式分别为：

$w^{(l)}$ ~$N(0,\frac{2}{n^{(l)}})$ （1） $w^{(l)}$~ $U[- \frac { \sqrt 6}{n^{(l)}},\frac { \sqrt 6}{n^{(l)}}]$（2）

def get_fans(shape):
    fan_in = shape[0] if len(shape) == 2 else np.prod(shape[1:])
    fan_out = shape[1] if len(shape) == 2 else shape[0]
return fan_in, fan_out

def he_normal(shape, name=None):
    fan_in, fan_out = get_fans(shape)
    s = np.sqrt(2. / fan_in)
    return normal(shape, s, name=name)

def he_uniform(shape, name=None):
    fan_in, fan_out = get_fans(shape)
    s = np.sqrt(6. / fan_in)
return uniform(shape, s, name=name)

Orthogonal Initialization

Orthogonal初始化，又称为正交矩阵初始化。[4]

在反向传播的过程中要进行重复的矩阵乘法，而在对其SVD分解过程中，发现随着矩阵乘法次数N的逐渐增大：

• 如果所有的特征值的绝对值都小于1，那么矩阵F会逐渐消失。
• 如果所有的特征值的绝对值都等于1，那么矩阵F会保持在相应的常数范围内。
• 如果所有的特征值的绝对值都大于1，那么矩阵F会逐渐爆炸。

正交矩阵有许多有意思的特性，最重要的就是正交矩阵的特征值绝对值等于1。这意味着，无论我们重复多少次矩阵乘法，矩阵的结果既不会爆炸也不会消失。

def orthogonal(shape):
 
    flat_shape = (shape[0], np.prod(shape[1:]))
 
    a = np.random.normal(0.0, 1.0, flat_shape)
 
    u, _, v = np.linalg.svd(a, full_matrices=False)
 
    q = u if u.shape == flat_shape else v
 
    return q.reshape(shape)

梯度下降法的变种

在求解无约束优化问题时，梯度下降是最常采用的方法之一。如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解，反之如果是非凸函数也可以保证得到局部最优解。

Mini-batch

在第e个epoch时，在全部样本N中选取m个训练样本，计算梯度：

$$g_t = \frac{1}{m} \sum \frac{\partial J(\theta)}{\partial \theta} \\\\ \theta_t:=\theta_{t-1} - \alpha·g_t$$

其中，$\alpha$为学习率（$\alpha \geq 0$），$1 \leq m \leq N$。

BGD（m=N）

• 每一轮都用所有的样本去更新参数，降低计算效率
• 一旦跳入局部最优就无法跳出

SGD（m=1）

• 有一定几率跳出局部最优，到达更好的局部最优或者全局最优
• 引入噪声，具有正则化的效果
• 批量太小无法充分利用多核架构

合适的batch_size

深度学习中存在的一个问题：使用大的batchsize训练网络会导致网络的泛化性能下降（Generalization Gap）。文中给出了Generalization Gap现象的解释：大的batchsize训练使得目标函数倾向于收敛到sharp minima（类似于local minima），sharp minima导致了网络的泛化性能下降，同时文中给出了直观的数据支持。而小的batchsize则倾向于收敛到一个flat minima，这个现象支持了大家普遍认为的一个观点：小的batchsize存在固有噪声，这些噪声影响了梯度的变化。[5]

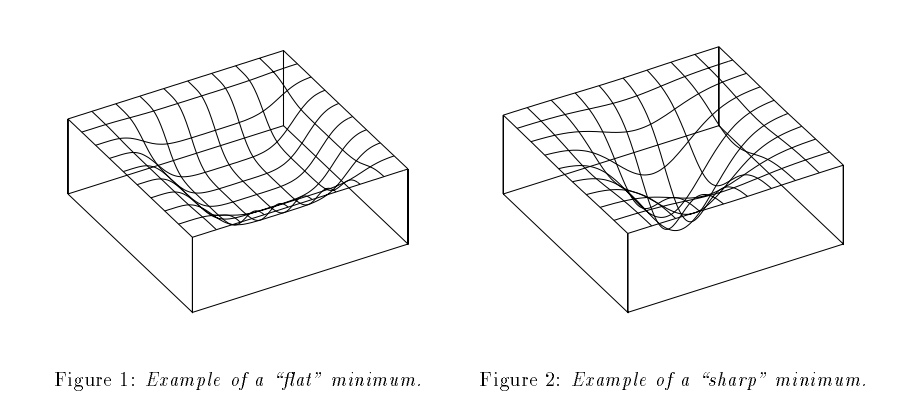
batchsize设置的不能太大也不能太小，GPU对2的幂次的batch可以发挥更佳的性能，因此设置成16、32、64、128…时往往要比设置为整10、整100的倍数时表现更优。（以下来自deeplearning.ai）首先，如果训练集较小，直接使用batch梯度下降法，样本集较小就没必要使用mini-batch梯度下降法，你可以快速处理整个训练集，所以使用batch梯度下降法也很好，这里的少是说小于2000个样本，这样比较适合使用batch梯度下降法。不然，样本数目较大的话，一般的mini-batch大小为64到512，考虑到电脑内存设置和使用的方式，如果mini-batch大小是2的$n$次方，代码会运行地快一些。

动量梯度下降法（Momentum）

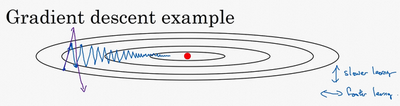
这种上下波动减慢了梯度下降法的速度，你就无法使用更大的学习率，如果你要用较大的学习率（紫色箭头），结果可能会偏离函数的范围，为了避免摆动过大，你要用一个较小的学习率。

下图的前两行公式为指数加权平均，此时的梯度不再只是现在的数据的梯度，而是有一定权重的之前的梯度。就像是把原本的梯度压缩一点，并且补上一个之前就已经存在的动量。每一次梯度下降都会有一个之前的速度的作用，如果我这次的方向与之前相同，则会因为之前的速度继续加速；如果这次的方向与之前相反，则会由于之前存在速度的作用不会产生一个急转弯，而是尽量把路线向一条直线拉过去。

$v_{dw}​$ 、$v_{db}​$的初始值为0，$\alpha​$、$\beta​$是超参数，$\beta​$通常取为0.9。

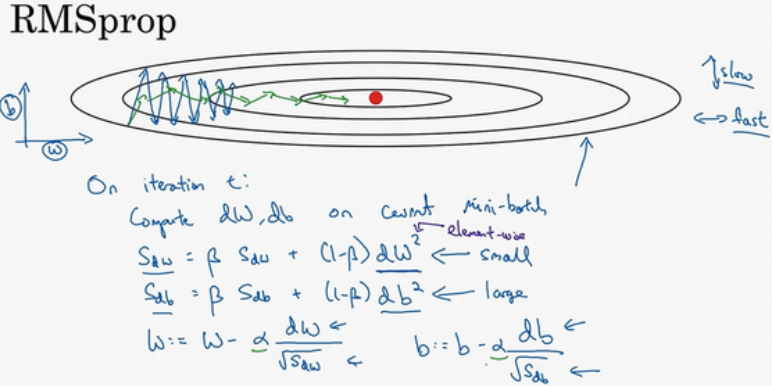
RMSprop

RMSprop 是 Geoff Hinton 提出的一种自适应学习率方法（自适应学习率对loss是不敏感的，换句话说，将loss乘上10倍，最终的优化效果基本没什么变化，但如果在随机梯度下降中，将loss乘上10倍，就等价于将学习率乘以10了）。根据历史梯度累积量来改变学习率。和动量梯度下降法一样，都解决了相同的问题，使梯度下降时的折返情况减轻，从而加快训练速度。因为下降的路线更接近同一个方向，因此也可以将学习率增大来加快训练速度。

AdaGrad

我们可以看出该优化算法与普通的sgd算法差别就在于标黄的哪部分，采取了累积平方梯度。[10]

简单来讲，设置全局学习率之后，每次通过，全局学习率逐参数的除以历史梯度平方和的平方根，使得每个参数的学习率不同。

正常情况下：

假设我们现在就只有两个参数w,b，我们从图中可以看到在b方向走的比较陡峭，这影响了优化速度。

而我们采取AdaGrad算法之后，我们在算法中使用了累积平方梯度r=:r + g.g。

从上图可以看出在b方向上的梯度g要大于在w方向上的梯度。

那么在下次计算更新的时候，r是作为分母出现的，越大的反而更新越小，越小的值反而更新越大，那么后面的更新则会像下面绿色线更新一样，明显就会好于蓝色更新曲线。

Adam

RMSProp + Momentum

初始化：$V_{dw}=0，S_{dw}=0，V_{db}=0，S_{db}=0​$

• 加速收敛
• 适合处理稀疏数据
• 自适应学习率
• 对大多数凸问题的优化有效

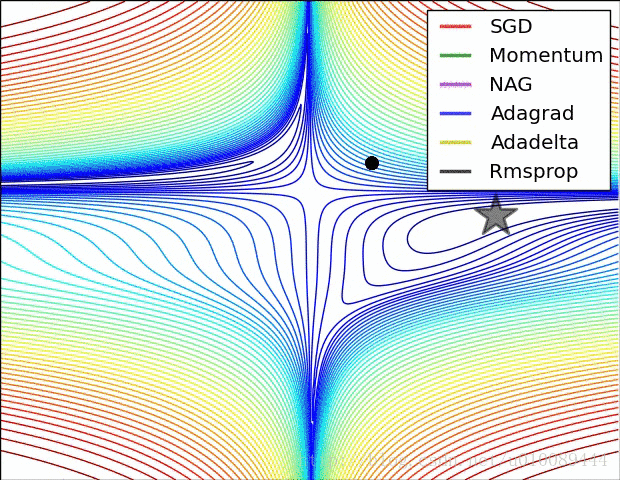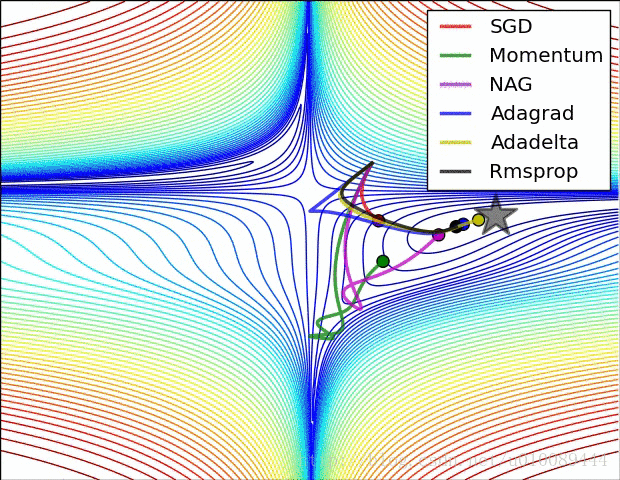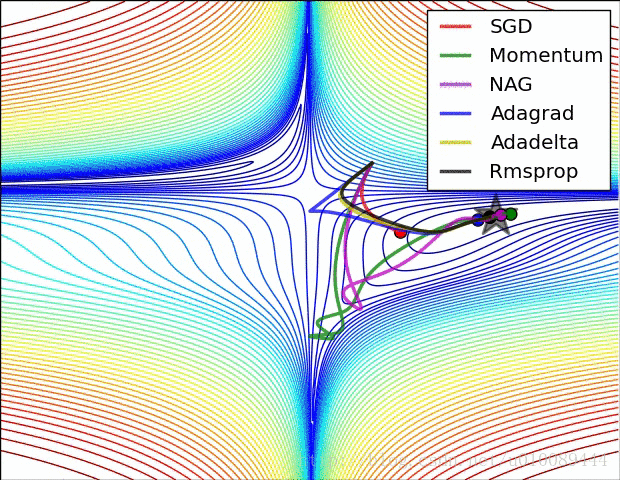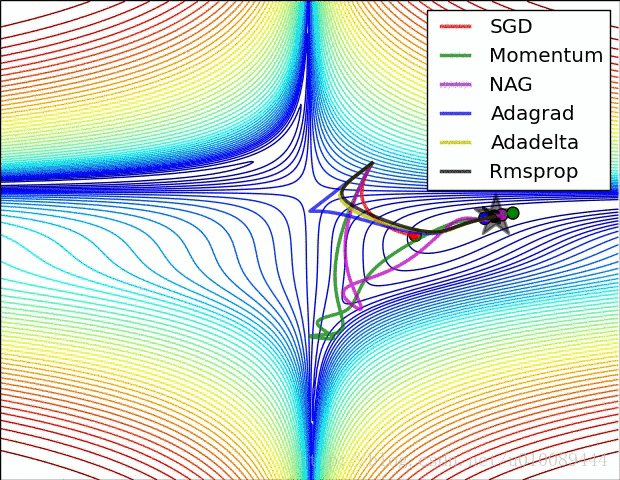
各种优化算法的对比

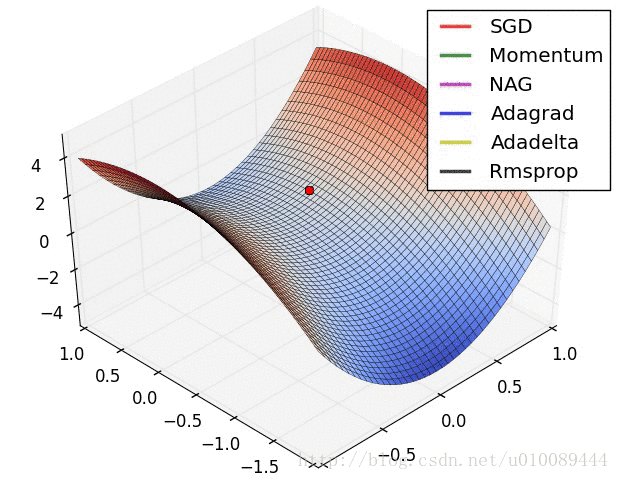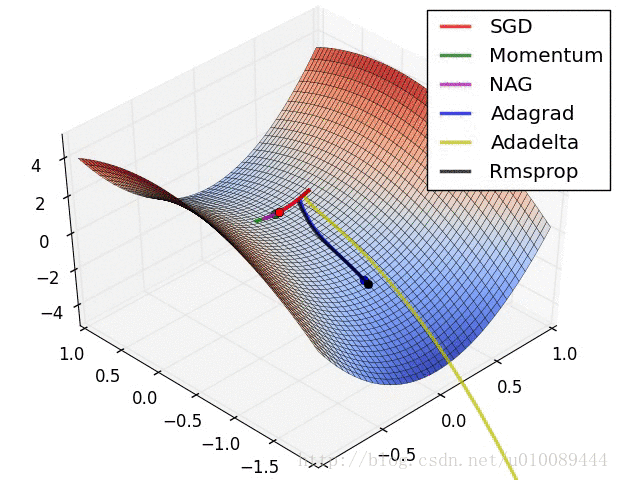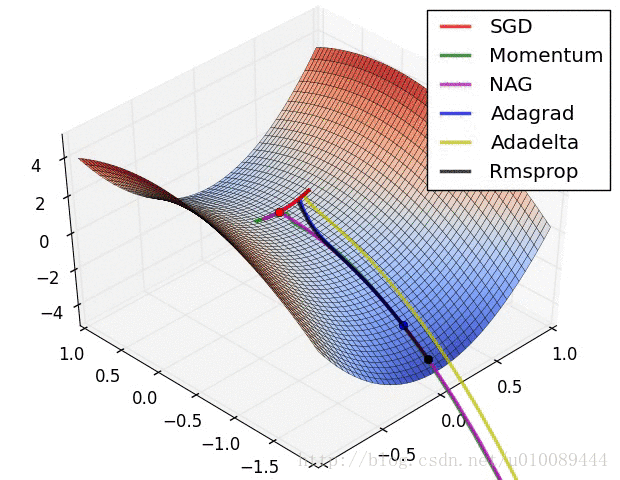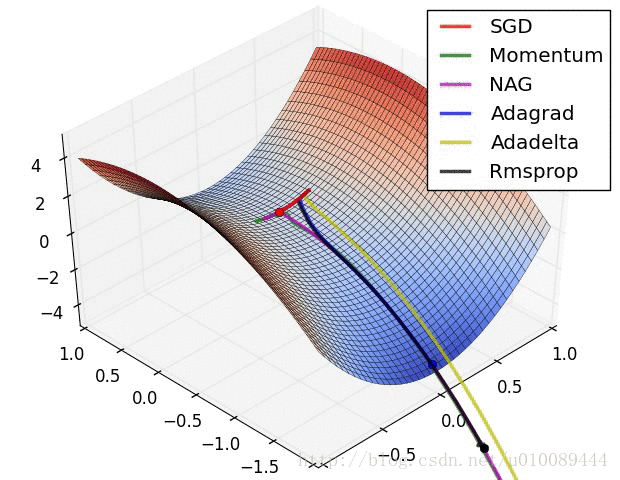
学习率衰减

将$a$学习率设为$\alpha= f({decay-rate,global-step}) * \alpha_0$ ，decay-rate称为衰减率，global_step为步数，$\alpha_0$为初始学习率，注意这个衰减率是另一个你需要调整的超参数。[6]

分段常数衰减就是在定义好的区间上，分别设置不同的常数值，作为学习率的初始值和后续衰减的取值。

指数衰减的学习速率计算公式为：

decayed_learning_rate = learning_rate * decay_rate ^ (global_step / decay_steps)

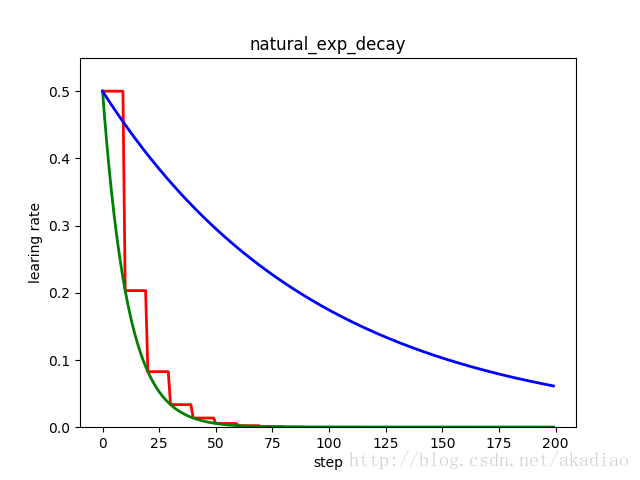
自然指数衰减的学习率计算公式为：

decayed_learning_rate = learning_rate * exp(-decay_rate * global_step)

红色：阶梯型；绿色：指数型；蓝色指数型衰减：

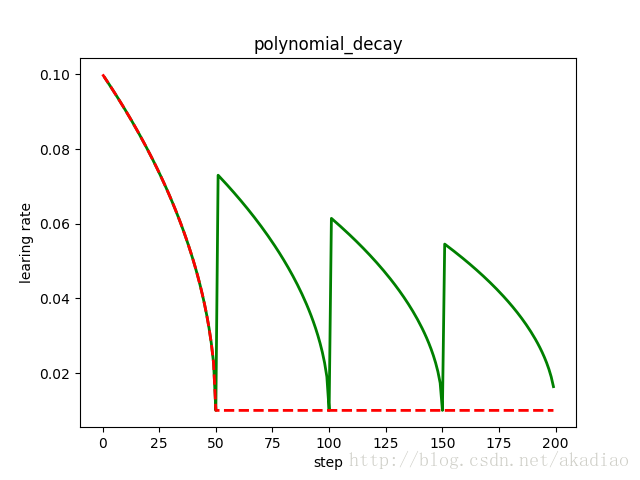
参数cycle决定学习率是否在下降后重新上升，若cycle为True，则学习率下降后重新上升；使用decay_steps的倍数，取第一个大于global_steps的结果。

decay_steps = decay_steps*ceil(global_step/decay_steps)

decayed_learning_rate = (learning_rate-end_learning_rate)*(1-global_step/decay_steps)^ (power)+end_learning_rate

参数cycle目的：防止神经网络训练后期学习率过小导致网络一直在某个局部最小值中振荡；这样，通过增大学习率可以跳出局部极小值．

红色：下降后不再上升；绿色：下降后重新上升：

梯度截断

在深层神经网络或循环神经网络中，除了梯度消失之外，梯度爆炸是影响学习效率的主要因素。在基于梯度下降的优化过程中，如果梯度突然增大，用大的梯度进行更新参数，反而会导致其远离最优点。为了避免这种情况，当梯度的模大于一定阈值时，就对梯度进行截断，称为梯度截断。

如何判断出现梯度爆炸：

• 训练过程中模型梯度快速变大
• 训练过程中模型权重变成 NaN 值
• 训练过程中，每个节点和层的误差梯度值持续超过1.0

按值截断 第t次迭代时，梯度为$g_t$，给定一个区间[a,b]，如果一个参数的梯度小于a，就将其设为a；如果小于b时，就将其设为b。

$$g_t = \max(\min(g_t,b),a)$$

按模截断 将梯度的模截断到一个给定的截断阈值b。

如果$||g_t||^2 \leq b$，保持$g_t$不变。如果$||g_t||^2 > b$，令

$$g_t = \frac{b}{||g_t||}g_t$$

在训练循环神经网络时，按模截断是避免梯度爆炸问题的有效方法。在 Keras 深度学习库中，你可以在训练之前设置优化器上的 clipnorm 或 clipvalue 参数，来使用梯度截断。

泛化问题

数据增强

图片处理：

• Color Jittering：对颜色的数据增强：图像亮度、饱和度、锐度、变焦；[7]
• PCA Jittering：首先按照RGB三个颜色通道计算均值和标准差，再在整个训练集上计算协方差矩阵，进行特征分解，得到特征向量和特征值，用来做PCA Jittering；
• Random Scale：尺度变换；
• Random Crop：采用随机图像差值方式，对图像进行裁剪、缩放；包括Scale Jittering方法（VGG及ResNet模型使用）或者尺度和长宽比增强变换；
• Horizontal/Vertical Flip：水平/垂直翻转；
• Shift：平移变换；
• Rotation/Reflection：旋转/仿射变换；
• Noise：高斯噪声、模糊处理

文本处理：

• clip|pad：对过长或过短的文本进行裁剪或者填充
• 随机dropout|替换：给定一个比例随机抽选文本dropout、或者替换成其他单词
• shuffle：打乱文本
• Noise：高斯噪音

正则化

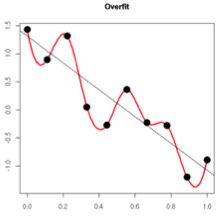
正则项的解释

可以从几个角度解释：

• 通过偏差方差分解去解释
• PAC-learning泛化界解释
• Bayes先验解释，把正则当成先验

从Bayes角度来看，正则相当于对模型参数引入先验分布：

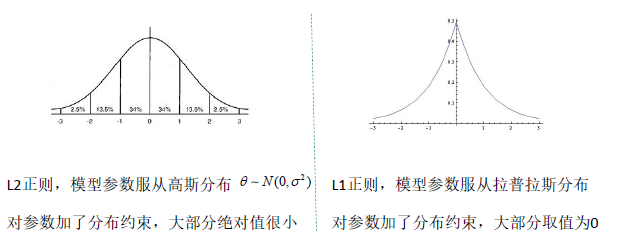
正则项的作用

（1）实现参数的稀疏，这样可以简化模型，避免过拟合。在一个模型中重要的特征并不是很多，如果考虑所有的特征都是有作用的，那么就会对训练集进行充分的拟合，导致在测试集的表现并不是很好，所以我们需要稀疏参数，简化模型。[8]
（2）尽可能保证参数小一些，这又是为啥呢？因为越是复杂的模型，它会对所有的样本点进行拟合，如果在这里包含异常的样本，就会在小区间内产生很大的波动，不同于平均水平的高点或者低点，这样的话，会导致其导数很大，我们知道在多项式导数中，只有参数非常大的时候，才会产生较大的导数，所以模型越复杂，参数值也就越大。为了避免这种过度的拟合，需要控制参数值的大小。

L1正则

$$C=C_0 +\frac{\lambda}{n}\sum_w|w| \\\\ \frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} sgn(w) \\\\ w :=w-\frac{\eta \lambda }{n}sgn(w)-\eta \frac{\partial C_0}{\partial w}$$

• 当w为正时，更新后的w变小；当w为负时，更新后的w变大。因此它的效果就是让w往0靠，使网络中的权重尽可能为0，也就相当于减小了网络复杂度，防止过拟合。
• w等于0时，|w|是不可导，可以规定$sgn(0)=0$，这样就把w=0的情况也统一进来了。

L2正则

L2范数是各参数的平方和再求平方根。对于L2的每个元素都很小，但是不会为0，只是接近0，参数越小说明模型越简单，也就越不容易产生过拟合。

$$J(\theta) = \frac{1}{2m}[\sum_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2 + \lambda\sum_{j=1}^n \theta_j^2]$$

λ 要做的就是控制惩罚项与均方差之间的平衡关系。

λ越大说明，参数被打压得越厉害，θ值也就越小

$$C=C_0 +\frac{\lambda}{2n}\sum_w w^2 \\\ \frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} w \\\\ w :=w-\frac{\eta \lambda }{n}w-\eta \frac{\partial C_0}{\partial w} \\\\ =(1-\frac{\eta \lambda}{n})w - \eta\frac{\partial C_0}{\partial w}$$

• 在不使用L2正则化时，求导结果中w前系数为1，现在w前面系数为 1-ηλ/n ，因为η、λ、n都是正的，在样本量充足的时候，1-ηλ/n小于1，它的效果是减小w，这也就是权重衰减的由来。

• 考虑到后面的导数项，w最终的值可能增大也可能减小

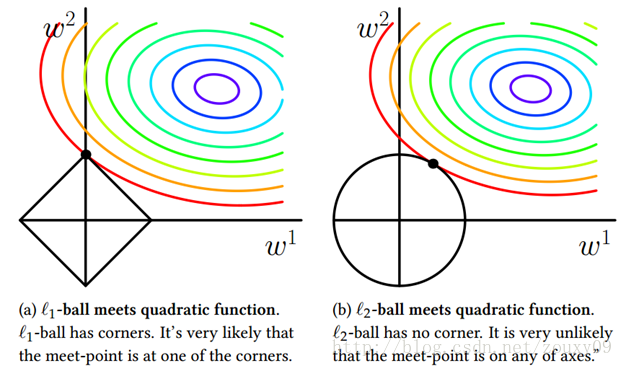
我们将模型空间限制在w的一个L1-ball 中。为了便于可视化，我们考虑两维的情况，在($w_1$,$ w_2$)平面上可以画出目标函数的等高线，而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解：

可以看到，L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现，而目标函数的测地线除非位置摆得非常好，大部分时候都会在角的地方相交。注意到在角的位置就会产生稀疏性，例如图中的相交点就有$w_1​$=0，而更高维的时候（想象一下三维的L1-ball 是什么样的？）除了角点以外，还有很多边的轮廓也是既有很大的概率成为第一次相交的地方，又会产生稀疏性。LASSO通常用来为其他方法所特征选择。例如，你可能会用LASSO回归获取适当的特征变量，然后在其他算法中使用。

相比之下，L2-ball 就没有这样的性质，因为没有角，所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小了。这就从直观上来解释了为什么L1-regularization 能产生稀疏性，而L2-regularization 不行的原因了。

从 Bayesian 的角度，可以认为L2正则和L1正则引入了不同的 prior（一个是 Gaussian 一个是 Laplacian）。

因此，一句话总结就是：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。

Dropout

Dropout会遍历网络的每一层，并设置消除神经网络中节点的概率。

假设网络中的每一层，每个节点都以抛硬币的方式设置概率，每个节点得以保留和消除的概率是p和1-p，设置完节点概率，我们会消除一些节点，然后删除掉从该节点进出的连线，最后得到一个节点更少，规模更小的网络，然后用backprop方法进行训练。

反向传播的时候，0的神经元的参数就不再更新。

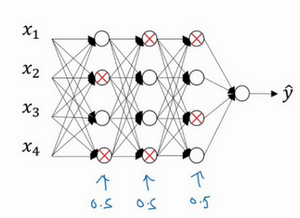
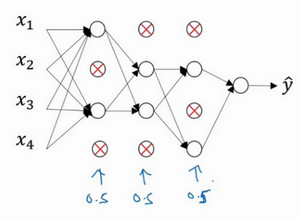
预测的时候，不使用Dropout（不对网络的参数做任何丢弃，就是说dropout layer进来什么就输出什么）。事实上，由于我们在测试时不使用Dropout，这样做导致统计意义下，测试时每层dropout layer比训练时的输出多加了(1-p)100% units的输出。所以，为了使得dropout layer下一层的输入和训练时具有相同的意义和数量级，我们对测试的伪dropout layer的输出做rescale：*乘以一个p，表示最后只有这么大的概率被保留下来。

假设x是dropout layer的输入，y是输出，W是上一层的weight params，$W|_p$是retaining probability为p采样得到的weight params子集，则有

$$train:y=W|_p*x\\\\ \ test:y = W*px$$

归一化

为什么需要归一化

• 神经网络学习过程本质就是为了学习数据分布，一旦训练数据与测试数据的分布不同，那么网络的泛化能力也大大降低
• 上层参数需要不断适应新的输入数据分布，降低学习速度。
• 下层输入的变化可能趋向于变大或者变小，导致上层落入饱和区，使得学习过早停止
• 每层的更新都会影响到其它层，因此每层的参数更新策略需要尽可能的谨慎

对于深度网络的训练是一个复杂的过程，只要网络的前面几层发生微小的改变，那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变，那么这一层网络就需要去适应学习这个新的数据分布，所以如果训练过程中，训练数据的分布一直在发生变化，那么将会影响网络的训练速度。

BatchNorm

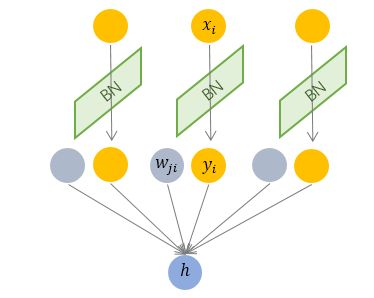
对每一个batch的输入都进行归一化，把数据转换为均值为0、方差为1的高斯分布。

$$\hat{x} = \frac{x-E(x)}{\sqrt{Var(x)+\epsilon}}$$

但是，强行归一化会破坏掉刚刚学习到的特征 ，把每层的数据分布都固定了，但不一定是前面一层学习到的数据分布。因此，设置两个可以学习的变量扩展参数$γ$ ，和平移参数 $β$ ，用这两个变量去还原上一层应该学习到的数据分布。[9]

$$y^{(k)} = \gamma^{(k)}\hat{x}^{(k)}+\beta^{(k)} \\\\$$

引入了这个可学习重构参数$γ、β$，让我们的网络可以学习恢复出原始网络所要学习的特征分布。最后Batch Normalization网络层的前向传导过程公式就是：

def Batchnorm_simple_for_train(x, gamma, beta, bn_param):
"""
param:x    : 输入数据，设shape(B,L)
param:gama : 缩放因子  γ
param:beta : 平移因子  β
param:bn_param   : batchnorm所需要的一些参数
	eps      : 接近0的数，防止分母出现0
	momentum : 动量参数，一般为0.9， 0.99， 0.999
	running_mean ：滑动平均的方式计算新的均值，训练时计算，为测试数据做准备
	running_var  : 滑动平均的方式计算新的方差，训练时计算，为测试数据做准备
"""
	running_mean = bn_param['running_mean']  #shape = [B]
    running_var = bn_param['running_var']    #shape = [B]
	results = 0. # 建立一个新的变量
    
	x_mean=x.mean(axis=0)  # 计算x的均值
    x_var=x.var(axis=0)    # 计算方差
    x_normalized=(x-x_mean)/np.sqrt(x_var+eps)       # 归一化
    results = gamma * x_normalized + beta            # 缩放平移

    running_mean = momentum * running_mean + (1 - momentum) * x_mean
    running_var = momentum * running_var + (1 - momentum) * x_var
    
    #记录新的值
    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var 
    
	return results , bn_param

优点

• Batchnorm本身上也是一种正则的方式，可以代替其他正则方式如dropout等
• 没有它之前，需要小心的调整学习率和权重初始化，但是有了BN可以放心的使用大学习率，但是使用了BN，就不用小心的调参了，较大的学习率极大的提高了学习速度

缺点

• 批量归一化是对一个中间层的单个神经元进行归一化操作，因此要求小批量样本的数量不能太小，否则难以计算单个神经元的统计信息

• 由于 BN 需要在运行过程中统计每个 mini-batch 的一阶统计量和二阶统计量，如果一个神经元的净输入的分布在神经网络中是动态变化的，比如循环神经网络，那么就无法应用批量归一化操作

位置

一般在全连接层和激活函数之间添加BN层

适用

每个 mini-batch 比较大，数据分布比较接近。在进行训练之前，要做好充分的 shuffle，否则效果会差很多。

LayerNorm

与 BN 不同，LN 是一种横向的规范化。

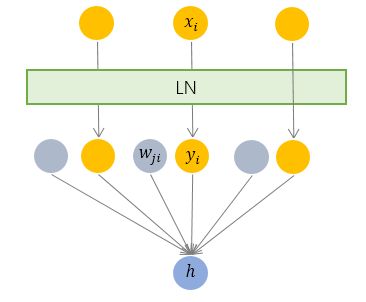
它综合考虑一层所有维度的输入，计算该层的平均输入值和输入方差，然后用同一个规范化操作来转换各个维度的输入。

对于一个深层神经网络中，令第$l$层神经的净输入为$z^{(l)}$，其均值和方差为：

$$\mu^{(l)} = \frac{1}{n^l}\sum_{i=1}^{n^l} z_i^{(l)} \\\\ \sigma^{(l)^2} = \frac{1}{n^l}\sum_{k=1}^{n^l} (z_i^{(l)}-\mu^{(l)})^2$$

其中$n^{l}​$为第l层神经元的数量。

层归一化的定义为：

$$\hat{z}^{(l)} = \frac{z^{(l)} - \mu^{(l)}}{\sqrt{\sigma^{(l)^2} + \epsilon}} \odot \gamma + \beta \\\\ =LayerNorm_{\gamma,\beta}(z^{l})$$

其中$\gamma$和$\beta$分别代表缩放和平移的参数向量。对循环神经层进行归一化操作。假设在时刻t，循环神经网络的隐藏层为$h_t$，其层归一化的更新为：

$$z_t = Uh_{t-1}+Wx_t \\\\ h_t = f(LN_{\gamma,\beta}(z_t))$$

其中输入为$x_t$为第$t$时刻的输入，U、W为网络参数。

Early Stop

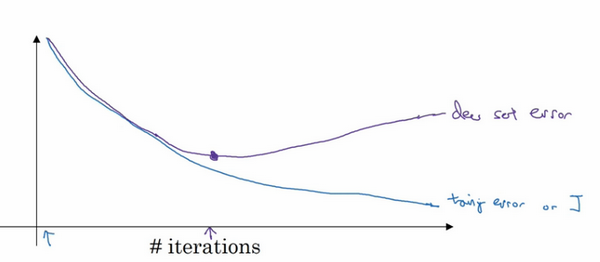
当你还未在神经网络上运行太多迭代过程的时候，参数$w$接近0，因为随机初始化$w$值时，它的值可能都是较小的随机值，所以在你长期训练神经网络之前$w$依然很小，在迭代过程和训练过程中$w$的值会变得越来越大，比如在这儿，神经网络中参数$w$的值已经非常大了，所以early stopping要做就是在中间点停止迭代过程。

early stopping的主要缺点就是你不能独立地处理这两个问题，因为提早停止梯度下降，也就是停止了优化代价函数$J$，因为现在你不再尝试降低代价函数$J$，所以代价函数$J$的值可能不够小，同时你又希望不出现过拟合，你没有采取不同的方式来解决这两个问题，而是用一种方法同时解决两个问题，这样做的结果是我要考虑的东西变得更复杂。

Early stopping的优点是，只运行一次梯度下降，你可以找出$w$的较小值，中间值和较大值，而无需尝试$L2$正则化超级参数$\lambda$的很多值。

参考资料：

[1]. [DL]扯扯神经网络的优化理论

[2]. 为什么损失函数是非凸的

[3]. 初始化方法

[4]. 正交矩阵初始化1 正交矩阵初始化2

[5]. batch_size

[6]. 学习率衰减

[7]. 图片数据增强

[8]. 正则项

[9]. 批归一化

[10]. Adagrad

[n]. deeplearning.ai