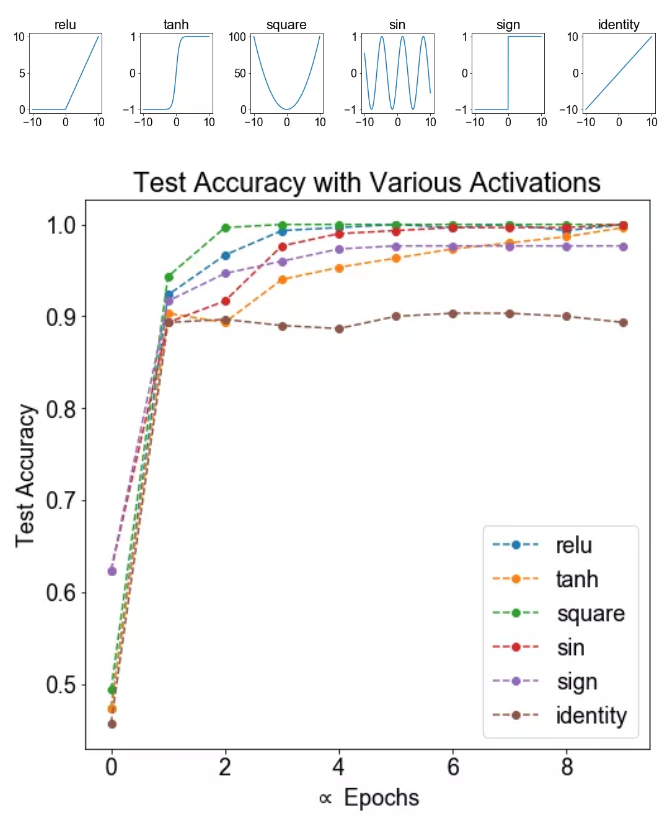
使用激活函数的目的

事实证明，如果你使用线性激活函数(恒等激励函数)或者没有使用一个激活函数，那么无论你的神经网络有多少层一直在做的只是计算线性函数，所以不如直接去掉全部隐藏层。在我们的简明案例中，事实证明如果你在隐藏层用线性激活函数，在输出层用Sigmoid函数，那么这个模型的复杂度和没有任何隐藏层的标准Logistic回归是一样的。

在这里线性隐层一点用也没有，因为这两个线性函数的组合本身就是线性函数，所以除非你引入非线性，否则你无法计算更有趣的函数，即使你的网络层数再多也不行；只有一个地方可以使用线性激活函数———，就是你在做机器学习中的回归问题。是一个实数，举个例子，比如你想预测房地产价格，就不是二分类任务0或1，而是一个实数，从0到正无穷。如果是个实数，那么在输出层用线性激活函数也许可行，你的输出也是一个实数，从负无穷到正无穷。

总而言之，不能在隐藏层用线性激活函数，可以用ReLU或者tanh或者leaky ReLU或者其他的非线性激活函数，唯一可以用线性激活函数的通常就是输出层；除了这种情况，会在隐层用线性函数的，在这之外，在隐层使用线性激活函数非常少见。

Sigmoid函数

Sigmoid函数是深度学习领域开始时使用频率最高的激活函数。

函数形式

$\sigma(x) = \frac{1}{1+e^{-x}}$ $\sigma'(x) = \sigma(x)(1-\sigma(x))$

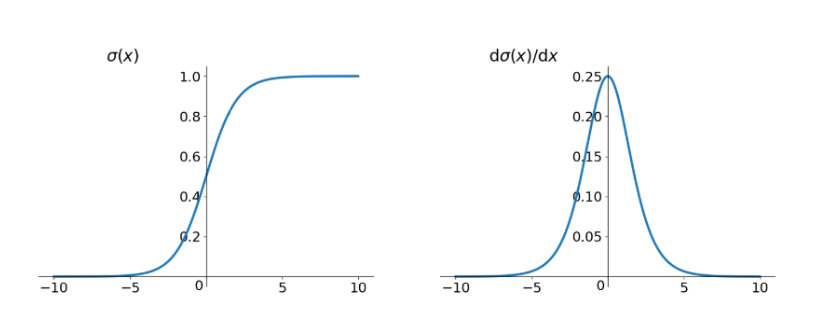
Sigmoid梯度消失的原因

首先看一个简单的深度神经网络，每一层都只有一个简单的神经元，那么关于$b_1$的梯度，根据链式求导法则为：

$\frac{\partial C}{\partial b_1} = \sigma'(z_1)w_2\sigma'(z_2)w_3\sigma'(z_3)w_4\sigma'(z_4) \frac{\partial C}{\partial a_4}$

根据上图的Sigmoid函数求导的曲线，该导数在$\sigma’(0) = \frac{1}{4}$时达到最高。如果我们初始化网络中的权重，假设初始化方法为均值为0方差为1的正态分布，那么所有的权重都会满足$w<1$。那么参数求导的过程中，$\sigma’(z_j)w_j<\frac{1}{4}$，并且随着参数项的叠加，乘积也在不断下降，最终$\frac{\partial C}{\partial b_1}$要远远小于1/4。

zero-centered

Sigmoid函数的输出值恒大于0，会导致模型训练的收敛速度变慢。比如下图所示，显然并非一个好的优化路径。

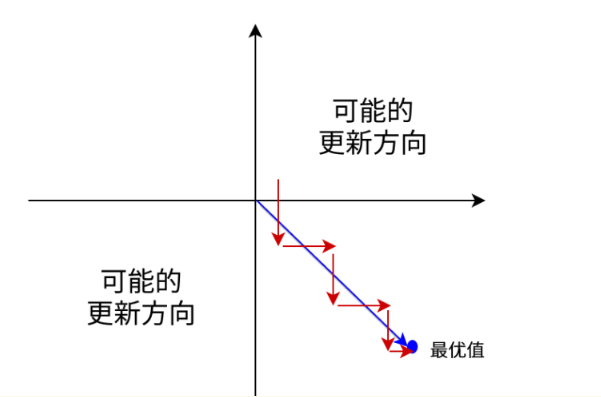
Sigmoid 函数包含 exp 指数运算，运算成本也比较大。

Tanh函数

Tanh函数即双曲正切函数。

函数形式

$tanh(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$ $tanh'(x) = 1-(tanh(x))^2$

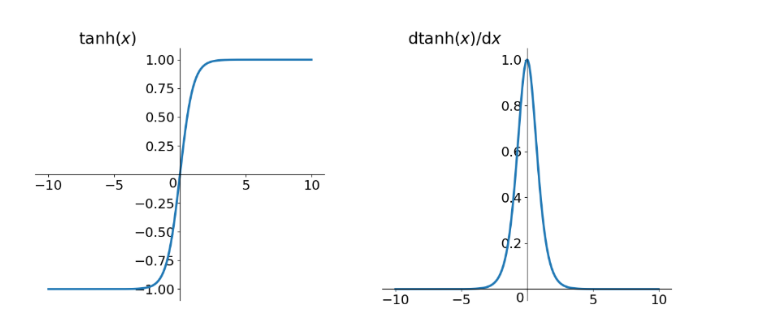
扩展

$\int tanh\ x \ dx= ln(cosh \ x) +C$

公式证明：http://math2.org/math/integrals/more/tanh.htm

评价

优点：解决了zero-centered的输出问题

缺点：梯度消失的问题和幂运算的问题仍然存在，其饱和区甚至比 Sigmoid 还要大一些，但不明显。

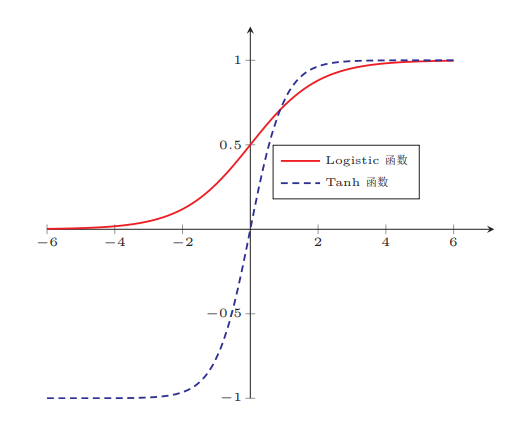
Tanh与Sigmoid

RNN中的Tanh函数

循环神经网络用的激活函数经常是Tanh，不过有时候也会用ReLU，但是Tanh是更通常的选择，我们有其他方法来避免梯度消失问题。另外，RNN中的激活函数是可以改的，如果采用Relu函数的话，注意梯度爆炸的时候要采用梯度修剪。

事实上梯度消失在训练RNN时是首要的问题，尽管梯度爆炸也是会出现，但是梯度爆炸很明显，因为指数级大的梯度会让你的参数变得极其大，以至于你的网络参数崩溃。所以梯度爆炸很容易发现，因为参数会大到崩溃，你会看到很多NaN，或者不是数字的情况，这意味着你的网络计算出现了数值溢出。如果你发现了梯度爆炸的问题，一个解决方法就是用梯度修剪。梯度修剪的意思就是观察你的梯度向量，如果它大于某个阈值，缩放梯度向量，保证它不会太大，这就是通过一些最大值来修剪的方法。所以如果你遇到了梯度爆炸，如果导数值很大，或者出现了NaN，就用梯度修剪，这是相对比较鲁棒的，这是梯度爆炸的解决方法。

Relu函数

Relu函数其实就是一个取最大值函数，这并不是全区间可导的。

函数形式

$Relu = max(0,x)$

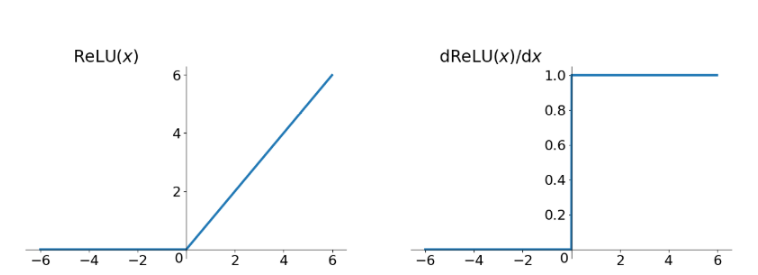
评价

优点：

解决了梯度消失的问题（正区间）
计算简单，速度非常快
收敛速度远快于Sigmoid和Tanh

缺点：

输出不是zero-centered
Dead Relu Problem

Dead Relu Problem是指某些神经元可能永远都不会被激活，导致相应的参数永远都不能被更新。有主要两个原因可能导致：1、非常不幸的参数初始化 2、学习速率太高导致。

$y = Wx+b \\ W:W-\eta*\frac{dL}{dW}$

当学习率$\eta$大的时候，W会变成负数，导致relu(y)=0。解决方法是采用HE初始化方法，以及避免将学习速率设置太大。如果不好解决，可以试试 Leaky ReLU、PReLU 或者 Maxout。

xavier初始化对Tanh有效

he初始化对Relu 有效

为什么he或者xavier初始化有效？（参考deeplearning,ai的解释）

$z = w_1 x_1 +w_2 x_2 +…+ w_n x_n$，暂时忽略$b$，为了预防$z$值过大或过小，可以看到当n越大，你希望$w_i$越小，因为z是$w_i x_i$的和，如果你把很多此类项相加，希望每项值更小，那么最合理的方法就是$w_i = \frac{1}{n}$，n表示神经元的输入特征数量，实际上，你要做的就是设置某层权重矩阵$w^{[l]} = np.random.randn( \text{shape}) * \text{np.}\text{sqrt}(\frac{1}{n^{[l-1]}})$，$n^{[l - 1]}$就是我喂给第$l$层神经单元的数量（即第$l-1$层神经元数量）。

Leaky Relu函数

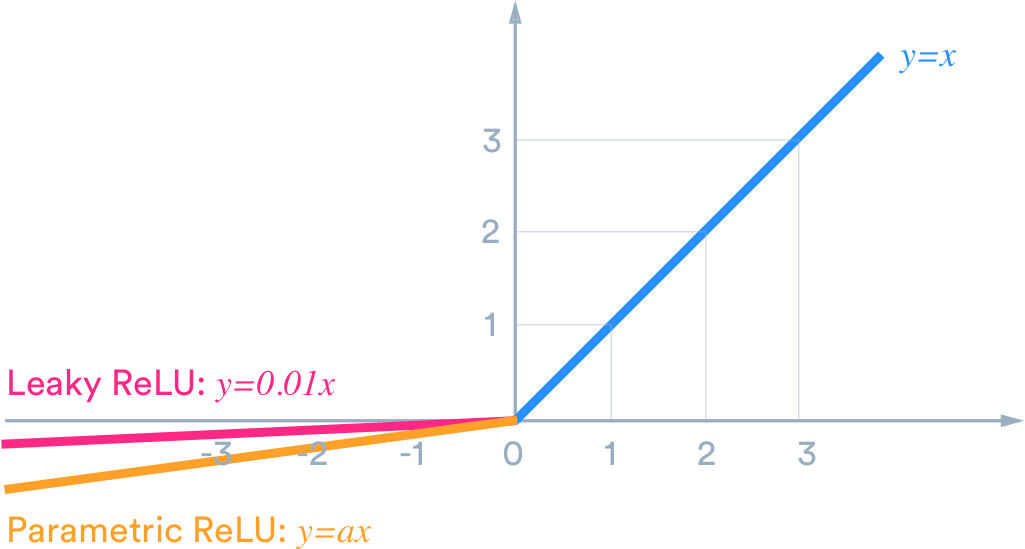
Leaky Relu在输入x<0时，保持一个很小的梯度$\lambda$。这样当神经元非激活时也能有一个非零的梯度可以更新参数，避免永远不能激活。

$Leaky Relu(x) = \left\{ \begin{aligned} x ,if\ x>0 \\ \gamma x,if \ x\leq0 \end{aligned} \right. \\\\=\max(0,x) +\gamma \min (0,x)$

$\gamma$是个很小的参数，比如0.01。

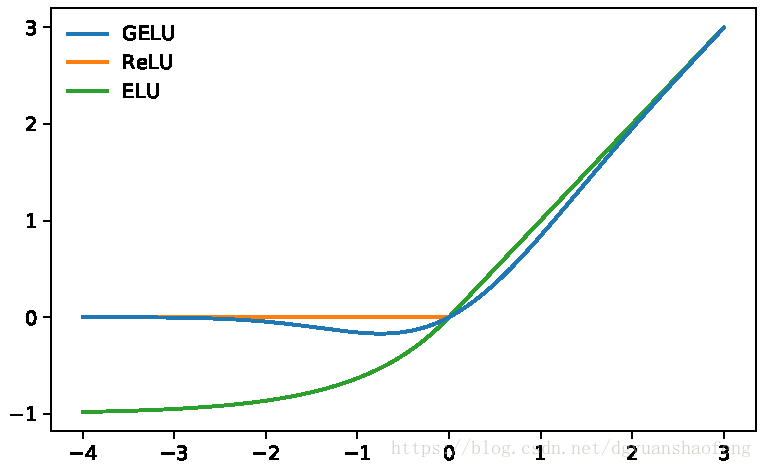
Gelu函数

GELU高斯误差线性单元bridge确定性激活函数ReLU和随机正则子Dropout之间的gap，也就是希望GELU这种随机性激活函数替代ReLU。

函数形式

$Gelu(x) = xP(X\leq x)，X服从N(\mu,\sigma^2)$

Gelu对于输入乘以依概率随机的概率分布$\Phi(x) = P(X\leq x)$，这里$\Phi(x)$是正太分布的概率函数，可以简单采用正太分布N(0,1)。

代码实现

#tensorflow
def gelu(input_tensor):
	cdf = 0.5 * (1.0 + tf.erf(input_tensor / tf.sqrt(2.0)))
	return input_tesnsor*cdf

一些问题

是否可以将任何非线性作为激活函数?